某群体的人均通勤时间,是指单日内该群体中成员从居住地到工作地的平均用时,某地上班族S中的成员仅以自驾或公交方式通勤,分析显示:当S中 的成员自驾时,自驾群体的人均通勤时间为
(单位:分钟),
而公交群体的人均通勤时间不受x影响,恒为40分钟,试根据上述分析结果回答下列问题:
(1)当x在什么范围内时,公交群体的人均通勤时间少于自驾群体的人均通勤时间?
(2)求该地上班族S的人均通勤时间 的表达式;讨论 的单调性,并说明其实际意义。
已知数列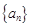 是首项
是首项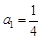 的等比数列,其前
的等比数列,其前 项和
项和 中
中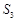 ,
,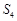 ,
, 成等差数列,
成等差数列,
(1)求数列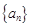 的通项公式;
的通项公式;
(2)设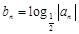 ,若
,若 ,求证:
,求证: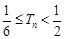 .
.
己知在锐角ΔABC中,角 所对的边分别为
所对的边分别为 ,且
,且
(Ⅰ)求角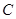 大小;
大小;
(Ⅱ)当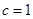 时,求
时,求 的取值范围.
的取值范围.
.已知圆 ,直线
,直线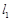 过定点 A (1,0).
过定点 A (1,0).
(1)若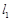 与圆C相切,求
与圆C相切,求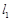 的方程;
的方程;
(2)若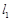 的倾斜角为
的倾斜角为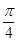 ,
,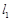 与圆C相交于P,Q两点,求线段PQ的中点M的坐标;
与圆C相交于P,Q两点,求线段PQ的中点M的坐标;
(3)若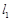 与圆C相交于P,Q两点,求△CPQ面积的最大值
与圆C相交于P,Q两点,求△CPQ面积的最大值
如图,已知 中,
中, ,
, 斜边
斜边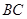 上的高,以
上的高,以 为折痕,将
为折痕,将 折 起,使
折 起,使 为直角。
为直角。
(1)求证:平面 平面
平面 ;(2)求证:
;(2)求证:
(3) 求点 到平面
到平面 的距离;(4) 求点
的距离;(4) 求点 到平面
到平面 的距离;
的距离;

已知直线l过点P(3,4)
(1)它在y轴上的截距是在x轴上截距的2倍,求直线l的方程.
(2)若直线l与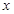 轴,
轴, 轴的正半轴分别交于点
轴的正半轴分别交于点 ,求
,求 的面积的最小值.
的面积的最小值.