在数列
中,
,且对任意
成等差数列,其公差为
.
(Ⅰ)若
,证明
成等比数列(
)
(Ⅱ)若对任意
,
成等比数列,其公比为
.证明:对任意
,有
已知函数 .
(Ⅰ)求函数
的单调区间和极值;
(Ⅱ)已知函数
的图象与函数
的图象关于直线
对称,证明当
时,
(Ⅲ)如果 ,且 ,证明
已知椭圆
的离心率
,连接椭圆的四个顶点得到的菱形的面积为4。
(1)求椭圆的方程;
(2)设直线
与椭圆相交于不同的两点
,已知点
的坐标为
,点
在线段
的垂直平分线上,且
,求
的值
如图,在长方体 中, 分别是棱 上的点, .
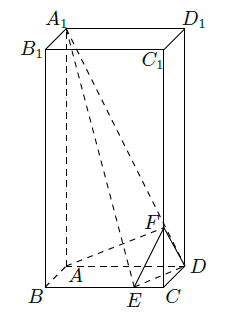
(1)求异面直线
与
所成角的余弦值;
(2)证明
平面
;
(3)求二面角 的正弦值.
某射手每次射击击中目标的概率是
,且各次射击的结果互不影响。
(Ⅰ)假设这名射手射击5次,求恰有2次击中目标的概率
(Ⅱ)假设这名射手射击5次,求有3次连续击中目标。另外2次未击中目标的概率;
(Ⅲ)假设这名射手射击3次,每次射击,击中目标得1分,未击中目标得0分,在3次射击中,若有2次连续击中,而另外1次未击中,则额外加1分;若3次全击中,则额外加3分,记
为射手射击3次后的总的分数,求
的分布列。