设数列满足 , .
(1)求证:
(2)若 , , 证明: .
(本题12分)如图,斜三棱柱 的底面是直角三角形,
的底面是直角三角形, ,点
,点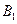 在底面
在底面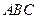 上的射影恰好是
上的射影恰好是 的中点,且
的中点,且 .
.
(Ⅰ)求证:平面 平面
平面 ;
;
(Ⅱ)求证: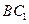
 ;
;
(Ⅲ)求二面角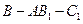 的大小.
的大小. 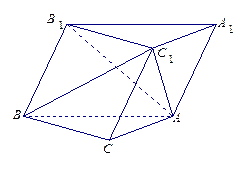
(本题12分) 某次演唱比赛,需要加试文化科学素质,每位参赛选手需加答3个问题,组委会为每位选手都备有10道不同的题目可供选择,其中有5道文史类题目,3道科技类题目,2道体育类题目,测试时,每位选手从给定的10道题中不放回地随机抽取3次,每次抽取一道题,回答完该题后,再抽取下一道题目作答.
(Ⅰ)求某选手第二次抽到的不是科技类题目的概率;
(Ⅱ)求某选手抽到体育类题目数 的分布列和数学期望E
的分布列和数学期望E .
.
(本题10分) 在 中,内角
中,内角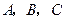 对边的边长分别是
对边的边长分别是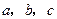 ,已知
,已知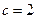 ,
, .
.
(Ⅰ)若 的面积等于
的面积等于 ,求
,求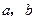 ;
;
(Ⅱ)若 ,求
,求 的面积.
的面积.
(本小题满分7分)选修 ;不等式选讲
;不等式选讲
已知 为正实数,且
为正实数,且 ,求
,求 的最小值及取得最小值时
的最小值及取得最小值时 的值.
的值.
(本小题满分7分)选修4-4:坐标系与参数方程
已知极坐标系的极点在直角坐标系的原点 处,极轴与
处,极轴与 轴的正半轴重合.直线l的极坐标方程为
轴的正半轴重合.直线l的极坐标方程为 ,圆
,圆 的参数方程为
的参数方程为 (参数
(参数 ),求圆心
),求圆心 到直线
到直线 的距离.
的距离.