已知函数 .
(1)求 的单调递增区间;
(2)设△ABC为锐角三角形,角A所对边 ,角B所对边b=5,若 ,求△ABC的面积.
已知等差数列{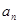 }中,
}中,
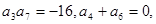 求{
求{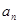 }前n项和
}前n项和 . .
. .
已知椭圆C的离心率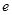 =
=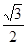 ,长轴的左右两个端点分别为
,长轴的左右两个端点分别为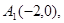
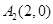 ;
;
(1)求椭圆C的方程;
(2)点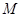 在该椭圆上,且
在该椭圆上,且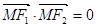 ,求点
,求点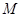 到
到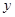 轴的距离;
轴的距离;
(3)过点(1,0)且斜率为1的直线与椭圆交于P,Q两点,求△OPQ的面积.
如图, 在直三棱柱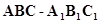 中,
中,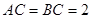 ,
,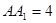 ,
, 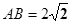 ,点
,点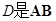 的中点,
的中点,
(I)求证: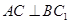
(II)求证: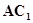 //平面
//平面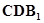 ;
;
(Ⅲ)求几何体 的体积.
的体积.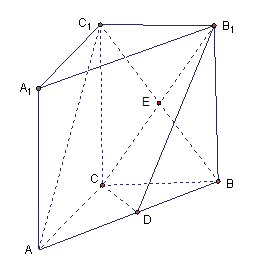
已知向量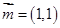 ,向量
,向量 与向量
与向量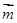 的夹角为
的夹角为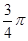 ,且
,且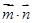
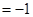 ;
;
(1)求向量 ;
;
(2)设向量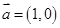 ,向量
,向量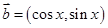 ,其中
,其中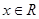 ,若
,若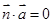 ,试求
,试求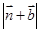 的取值范围。
的取值范围。
甲打靶射击,有4发子弹,其中有一发是空弹
(1)求空弹出现在第一枪的概率;
(2)求空弹出现在前三枪的概率;
(3)如果把空弹换成实弹,甲前三枪在靶上留下三个两两距离分别为3,4,5的弹孔P、Q、R(如图),第四枪瞄准了三角形PQR射击,第四个弹孔落在三角形PQR内,求第四个弹孔与前三个弹孔的距离都超过1的概率(忽略弹孔大小).