如图,四棱锥 中, , , , ,M为线段AD上一点, ,N为PC的中点.

(1)证明 ;
(2)求四面体 的体积.
已知非零向量a,b,且a⊥b,求证: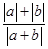 ≤
≤ .
.
已知函数f(x)=ax+ (a>1).
(a>1).
(1)证明:函数f(x)在(-1,+∞)上为增函数;
(2)用反证法证明方程f(x)=0没有负数根.
已知x∈R,a=x2+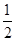 ,b=2-x,c=x2-x+1,试证明a,b,c至少有一个不小于1.
,b=2-x,c=x2-x+1,试证明a,b,c至少有一个不小于1.
蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似地看作是一个正六边形,如图为一组蜂巢的截面图.其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,以f(n)表示第n个图的蜂巢总数.
(1)试给出f(4),f(5)的值,并求f(n)的表达式(不要求证明);
(2)证明: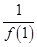 +
+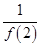 +
+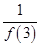 +…+
+…+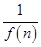 <
<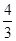 .
.
某少数民族的刺绣有着悠久的历史,如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都是由小正方形构成,小正方形数越多刺绣越漂亮.现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.
(1)求出f(5)的值;
(2)利用合情推理的“归纳推理思想”,归纳出f(n+1)与f(n)之间的关系式,并根据你得到的关系式求出f(n)的表达式;
(3)求 +
+ +
+ +…+
+…+ 的值.
的值.