在平面直角坐标系
中,已知直线l的参数方程为
(t为参数),曲线C的参数方程为
(s为参数).设P为曲线C上的动点,求点P到直线l的距离的最小值.
如图,多边形ABCDE中,∠ABC=90°,AD∥BC,△ADE是正三角形,AD=2,AB=BC=1,沿直线AD将△ADE折起至△ADP的位置,连接PB,BC,构成四棱锥P-ABCD,使得∠PAB=90°.点O为线段AD的中点,连接PO.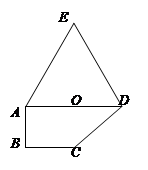
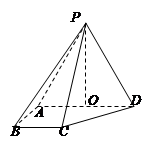
(1)求证:PO⊥平面ABCD;
(2)求异面直线CD与PA所成角的余弦值.
设关于x的一元二次方程x2+2ax+b2=0
(1)若a是从0,1,2,3四个数中任取的一个数,b是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
(2)若a是从区间[0,3]任取的一个实数,b是从区间[0,2]任取的一个实数,求上述方程有实根的概率.
已知点P(x1,y1),Q(x2,y2)是函数f(x)=sin(ωx+Φ)(ω>0,0<Φ<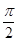 )图象上的任意两点,若|y1-y2|=2时,|x1-x2|的最小值为
)图象上的任意两点,若|y1-y2|=2时,|x1-x2|的最小值为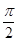 ,且函数f(x)的图象经过点(0,2),在△ABC中,角A,B,C的对边分别为a,b,c,且2sinAsinC+cos2B=1.
,且函数f(x)的图象经过点(0,2),在△ABC中,角A,B,C的对边分别为a,b,c,且2sinAsinC+cos2B=1.
(1)求函数f(x)的解析式;
(2)求g(B)= f(B)+f(B+
f(B)+f(B+ )的取值范围.
)的取值范围.
已知函数f(x)=lnx+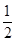 ax2-(a+1)x(a∈R).
ax2-(a+1)x(a∈R).
(1)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)当a>0时,若f(x)在区间[1,e]上的最小值为-2,求实数a的值;
(3)若对"x1,x2∈(0,+∞),x1<x2,且f(x1)+x1<f(x2)+x2恒成立,求实数a的取值范围.
已知函数f(x)=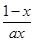 +lnx.
+lnx.
(1)若函数f(x)在[1,+∞)上为增函数,求实数a的取值范围;
(2)设数列{bn}的前n项和为Sn,其中bn=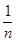 ,求证:当n≥2时,1+lnn>Sn.
,求证:当n≥2时,1+lnn>Sn.