已知a,b,c,d为实数,且
,
,证明
.
(本小题满分14分)
函数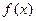 定义在区间[a, b]上,设“
定义在区间[a, b]上,设“ ”表示函数
”表示函数 在集合D上的最小值,“
在集合D上的最小值,“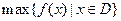 ”表示函数
”表示函数 在集合D上的最大值.现设
在集合D上的最大值.现设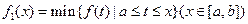 ,
,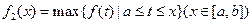 ,
,
若存在最小正整数k,使得 对任意的
对任意的 成立,则称函数
成立,则称函数 为区间
为区间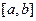 上的“第k类压缩函数”.
上的“第k类压缩函数”.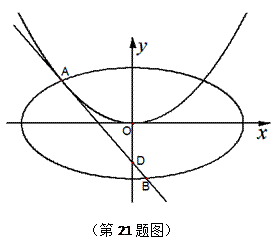
(Ⅰ) 若函数 ,求
,求 的最大值,写出
的最大值,写出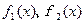 的解析式;
的解析式;
(Ⅱ) 若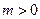 ,函数
,函数 是
是 上的“第3类压缩函数”,求m的取值范围.
上的“第3类压缩函数”,求m的取值范围.
(本小题满分15分)
已知点 ,过点
,过点 作抛物线
作抛物线
 的切线
的切线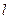 ,切点
,切点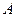 在第二象限,如图.(Ⅰ)求切点
在第二象限,如图.(Ⅰ)求切点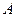 的纵坐标;
的纵坐标;
(Ⅱ)若离心率为 的椭圆
的椭圆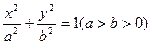 恰好经过切点
恰好经过切点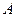 ,设切线
,设切线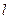 交椭圆的另一点为
交椭圆的另一点为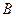 ,记切线
,记切线 的斜率分别为
的斜率分别为 ,若
,若 ,求椭圆方程.
,求椭圆方程.
(本小题满分15分)
如图,在四棱锥 中,底面
中,底面 为正方形,
为正方形,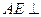 平面
平面 ,已知
,已知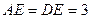 ,
, 为线段
为线段 上的动点.
上的动点.
(Ⅰ)若 为
为 的中点,求证:
的中点,求证: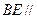 平面
平面 ;
;
(Ⅱ)若二面角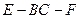 与二面角
与二面角 的大小相等,求
的大小相等,求 长.
长.
(本小题满分14分)
已知数列 的前
的前 项和为
项和为 ,
, ,若数列
,若数列 是公比为
是公比为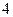 的等比数列.
的等比数列.
(Ⅰ)求数列 的通项公式
的通项公式 ;
;
(Ⅱ)设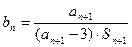 ,
, ,求数列
,求数列 的前
的前 项和
项和 .
.
(本小题满分14分)
在 中,角
中,角 所对的边分别为
所对的边分别为 ,且
,且 成等差数列.
成等差数列.
(Ⅰ)求角 的大小;(Ⅱ)若
的大小;(Ⅱ)若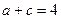 ,求
,求 边上中线长的最小值.
边上中线长的最小值.