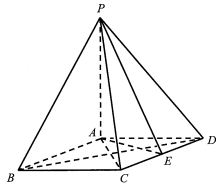
如图,在四棱锥 中, ,底部 ABCD为菱形, E为 CD的中点.
(Ⅰ)求证: ;
(Ⅱ)若 ,求证: ;
(Ⅲ)棱 PB上是否存在点 F,使得 ?说明理由.
(本小题满分13分)设函数 ,其中
,其中 为正整数.
为正整数.
(Ⅰ)判断函数 的单调性,并就
的单调性,并就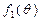 的情形证明你的结论;
的情形证明你的结论;
(Ⅱ)证明: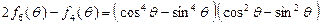 ;
;
(Ⅲ)对于任意给定的正整数 ,求函数
,求函数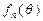 的最大值和最小值.
的最大值和最小值.
(本小题满分13分)椭圆 的左、右焦点分别为F1、F2,过F1的直线l与椭圆交于A、B两点.(Ⅰ)如果点A在圆
的左、右焦点分别为F1、F2,过F1的直线l与椭圆交于A、B两点.(Ⅰ)如果点A在圆 (c为椭圆的半焦距)上,且|F1A|=c,求椭圆的离心率;(Ⅱ)若函数
(c为椭圆的半焦距)上,且|F1A|=c,求椭圆的离心率;(Ⅱ)若函数 的图象,无论m为何值时恒过定点(b,a),求
的图象,无论m为何值时恒过定点(b,a),求 的取值范围.
的取值范围.
(本小题满分13分)已知数列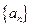 满足
满足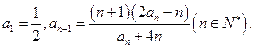
(Ⅰ)求 ;(Ⅱ)已知存在实数
;(Ⅱ)已知存在实数 ,使
,使 为公差为
为公差为 的等差数列,求
的等差数列,求 的值;
的值;
(Ⅲ)记 ,数列
,数列 的前
的前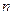 项和为
项和为 ,求证:
,求证: .
.
(本小题满分12分)如图,斜三棱柱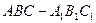 ,已知侧面
,已知侧面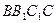 与底面ABC垂直且∠BCA =90°,∠
与底面ABC垂直且∠BCA =90°,∠ ,
, =2,若二面角
=2,若二面角 为30°.(Ⅰ)证明
为30°.(Ⅰ)证明 ;
; 
(Ⅱ)求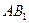 与平面
与平面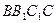 所成角的正切值;
所成角的正切值;
(Ⅲ)在平面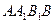 内找一点P,使三棱锥
内找一点P,使三棱锥 为正三棱锥,并求P到平面
为正三棱锥,并求P到平面 距离.
距离.
(本小题满分12分)在△OAB的边OA、OB上分别有一点P、Q,已知 :
: =1:2,
=1:2, 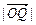 :
: =3:2,连结AQ、BP,设它们交于点R,若
=3:2,连结AQ、BP,设它们交于点R,若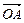 =a,
=a, =b.(Ⅰ)用a与 b表示
=b.(Ⅰ)用a与 b表示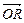 ;
;
(Ⅱ)过R作RH⊥AB,垂足为H,若| a|=1, | b|=2, a与 b的夹角 的范围.
的范围.