已知抛物线方程y24x，F为焦点，P为抛物线准线上一点，Q为-优题课

题文

已知抛物线方程 $y^{2} = 4 x$ ， $F$ 为焦点， $P$ 为抛物线准线上一点， $Q$ 为线段 $PF$ 与抛物线的交点，定义： $d (P) = \frac{| PF |}{| FQ |}$ ．

（1）当 $P (- 1, - \frac{8}{3})$ 时，求 $d (P)$ ；

（2）证明：存在常数 $a$ ，使得 $2 d (P) = | PF | + a$ ；

（3） $P_{1}$ ， $P_{2}$ ， $P_{3}$ 为抛物线准线上三点，且 $| P_{1} P_{2} | = | P_{2} P_{3} |$ ，判断 $d (P_{1}) + d (P_{3})$ 与 $2 d (P_{2})$ 的关系．

科目数学题型解答题难度中等

知识点：抛物线圆锥曲线综合

相关试题

已知
（1）证明：⊥；
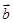（2）若存在实数k和t，满足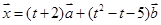且⊥，试求出k关于t的关系式k=f(t).
（3）根据（2）的结论，试求出k=f(t)在（－2，2）上的最小值.

二次函数f(x)满足f(x+1)-f(x)=2x,且f(0)=1.
（1）求f(x)的解析式；
（2）在区间[－1，1]上，y=f(x)的图象恒在y=2x+m的图象上方，求实数m的取值范围

如图，已知三棱锥P－ABC中，∠ACB＝90°，CB＝4，AB＝20，D为AB中点，M为PB中点，且△PDB是正三角形，PA⊥PC。
.
（1）求证：DM∥平面PAC；
（2）求证：平面PAC⊥平面ABC；
（3）求三棱锥M－BCD的体积

如图，在棱长为2的正方体ABCD－A₁B₁C₁D₁中，E为棱CC₁的中点。

（1）求证：BD⊥AE；
（2）求点A到平面BDE的距离．

如图，在四棱锥P－ABCD中，四边形ABCD是矩形，侧面PAD⊥底面ABCD，若点E，F分别是PC，BD的中点。

（1）求证：EF∥平面PAD；
（2）求证：平面PAD⊥平面PCD