图①是甘肃省博物馆的镇馆之宝 -- 铜奔马,又称 " 马踏飞燕 " ,于 1969 年 10 月出土于武威市的雷台汉墓, 1983 年 10 月被国家旅游局确定为中国旅游标志,在很多旅游城市的广场上都有 " 马踏飞燕 " 雕塑,某学习小组把测量本城市广场的 " 马踏飞燕 " 雕塑(图②)最高点离地面的高度作为一次课题活动,同学们制定了测量方案,并完成了实地测量,测得结果如下表:
课题 |
测量 " 马踏飞燕 " 雕塑最高点离地面的高度 |
|||
测量示意图 |
|
如图,雕塑的最高点 到地面的高度为 ,在测点 用仪器测得点 的仰角为 ,前进一段距离到达测点 ,再用该仪器测得点 的仰角为 ,且点 , , , , , 均在同一竖直平面内,点 , , 在同一条直线上. |
||
测量数据 |
的度数 |
的度数 |
的长度 |
仪器 ( )的高度 |
|
|
5 米 |
米 |
|
请你根据上表中的测量数据,帮助该小组求出 " 马踏飞燕 " 雕塑最高点离地面的高度(结果保留一位小数).(参考数据: , , , , , )

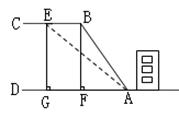
今年北京市大规模加固中小学校舍,房山某中学教学楼的后面靠近一座山坡,坡面上是一块平地,如图所示.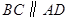 ,斜坡
,斜坡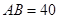 米,坡度i=
米,坡度i=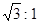 ,为防止山体滑坡,保障学生安全,学校决定不仅加固教学楼,还对山坡进行改造.经地质人员勘测,当坡角不超过
,为防止山体滑坡,保障学生安全,学校决定不仅加固教学楼,还对山坡进行改造.经地质人员勘测,当坡角不超过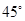 时,可确保山体不滑坡,改造时保持坡脚
时,可确保山体不滑坡,改造时保持坡脚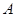 不动,从坡顶
不动,从坡顶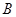 沿
沿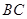 削进到
削进到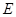 处,问
处,问 至少是多少米.(结果保留根号)
至少是多少米.(结果保留根号)
如图,在半径为r的半圆⊙O中,半径OA⊥直径BC,点E、F分别在弦AB、AC上滑动并保持AE=CF,但点F不与A、C重合,点E不与A、B重合.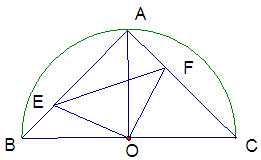
(1)求证 S四边形AEOF=
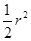 ;
;(2)设AE=x,S△OEF=y,写出y与x之间的函数关系式及自变量x的范围;
(3)当S△OEF =
 S△ABC时,求点E、F分别在AB、AC上的位置及EF的长。
S△ABC时,求点E、F分别在AB、AC上的位置及EF的长。
(8分)如图,在平面直角坐标系中,以点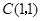 为圆心,以2为半径作圆,交
为圆心,以2为半径作圆,交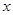 轴于
轴于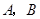 两点,开口向下的抛物线经过点
两点,开口向下的抛物线经过点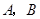 ,且其顶点
,且其顶点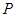 在⊙C上.
在⊙C上.
 |
(1)求
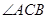 的大小;
的大小;(2)写出A、B两点的坐标;
(3)试确定此抛物线的解析式;
(4)在该抛物线上是否存在一点
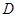 ,使线段
,使线段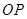 与
与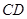 互相平分?若存在,求出点
互相平分?若存在,求出点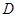 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
阅读材料,解答问题:
命题:如图,在锐角△ABC中,BC=a,CA=b,AB=c,ΔABC的外接圆半径为R,
则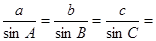 2R.
2R. 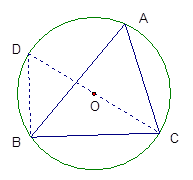
证明:连结CO并延长交⊙O于点D,连结DB,则∠D=∠A,因为CD是⊙O的直径,所以∠DBC=900,在Rt△DBC中,sinD=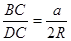 ,所以sinA=
,所以sinA=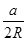 ,即
,即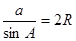 ,同理:
,同理: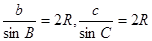 ,∴
,∴ 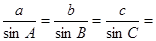 2R.
2R.
请阅读前面所给的命题和证明后,完成下面(1)(2)两题:(1)前面阅读材料中省略了“
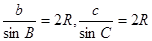 ”的证明过程,请你把“
”的证明过程,请你把“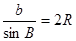 ”的证明过程补写出来.
”的证明过程补写出来. (2)直接运用阅读材料中命题的结论解题:已知锐角△ABC中, BC=
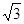 ,CA=
,CA=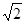 ,∠A=600,求△ABC的外接圆半径 R及∠C.
,∠A=600,求△ABC的外接圆半径 R及∠C.
如图,已知A、B、C、D均在已知圆上,AD‖BC,CA平分∠BCD,
∠ADC=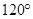 ,四边形ABCD周长为10.
,四边形ABCD周长为10.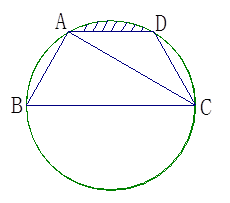
(1)求此圆的半径;
(2)求圆中阴影部分的面积.