在平面直角坐标系 中,点 在抛物线 上,设抛物线的对称轴为直线 .
(1)当 时,求抛物线与 轴交点的坐标及 的值;
(2)点 在抛物线上.若 ,求 的取值范围及 的取值范围.
某超市进了一批成本为6元/个的文具.调查后发现:这种文具每周的销售量y(个)与销售价x(元/个)之间的关系满足一次函数关系,如下表所示:
| 销售价x(元/个) |
8 |
9.5 |
11 |
14 |
| 销售量y(个) |
220 |
205 |
190 |
160 |
(1)求y与x之间的函数解析式(不必写出定义域);
(2)已知该超市这种文具每周的销售量不少于60个,若该超市某周销售这种文具(不考虑其它因素)的利润为800元,求该周每个文具的销售价.
如图,在△ABC中,AB=AC=10,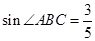 ,圆O经过点B、C,圆心O在△ABC的内部,且到点A的距离为2,求圆O的半径.
,圆O经过点B、C,圆心O在△ABC的内部,且到点A的距离为2,求圆O的半径.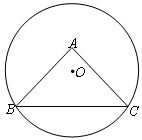
解方程组: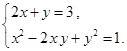
先化简,再求值: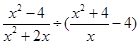 ,其中
,其中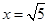 .
.
如图,反比例函数 y= 的图象与一次函数y=mx+b的图象交于两点A(1,3)、B(n,-1)
的图象与一次函数y=mx+b的图象交于两点A(1,3)、B(n,-1)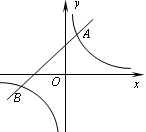
(1)求反比例函数与一次函数的函数关系式;
(2)根据图象,直接回答:当x取何值时,一次函数的值大于反比例函数的值;
(3)连接AO、BO,求△AOB的面积。