已知正方形ABCD,E为对角线AC上一点.
【建立模型】
(1)如图1,连接BE,DE.求证: ;
【模型应用】
(2)如图2,F是DE延长线上一点, ,EF交AB于点G.
①判断△FBG的形状并说明理由;
②若G为AB的中点,且AB=4,求AF的长.
【模型迁移】
(3)如图3,F是DE延长线上一点, ,EF交AB于点G, .求证: .

鲁南高铁临沂段修建过程中需要经过一座小山.如图,施工方计划沿 方向开挖隧道,为了加快施工速度,要在小山的另一侧 、 、 共线)处同时施工.测得 , , ,求 的长.

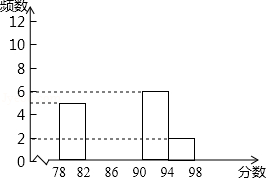
争创全国文明城市,从我做起,某学校在七年级开设了文明礼仪校本课程,为了解学生的学习情况,学校随机抽取30名学生进行测试,成绩如下(单位:分)
78 83 86 86 90 94 97 92 89 86 84 81 81 84 86 88 92 89 86 83 81 81 85 86 89 93 93 89 85 93
整理上面的数据得到频数分布表和频数分布直方图:
|
成绩(分 |
频数 |
|
|
5 |
|
|
|
|
|
11 |
|
|
|
|
|
2 |
回答下列问题:
(1)以上30个数据中,中位数是 ;频数分布表中 ; ;
(2)补全频数分布直方图;
(3)若成绩不低于86分为优秀,估计该校七年级300名学生中,达到优秀等级的人数.
解方程: .
如图,在平面直角坐标系中,抛物线 与 轴交于点 ,点 ,与 轴交于点 ,连接 .又已知位于 轴右侧且垂直于 轴的动直线 ,沿 轴正方向从 运动到 (不含 点和 点),且分别交抛物线、线段 以及 轴于点 , , .
(1)求抛物线的表达式;
(2)连接 , ,当直线 运动时,求使得 和 相似的点 的坐标;
(3)作 ,垂足为 ,当直线 运动时,求 面积的最大值.

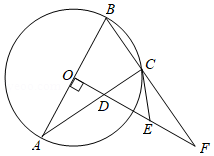
如图, 内接于 , 为直径,作 交 于点 ,延长 , 交于点 ,过点 作 的切线 ,交 于点 .
(1)求证: ;
(2)如果 , ,求弦 的长.