在一条笔直的滑道上有黑、白两个小球同向运动,黑球在 处开始减速,此时白球在黑球前面 处.

小聪测量黑球减速后的运动速度 (单位: )、运动距离 (单位: )随运动时间 (单位: )变化的数据,整理得下表.
运动时间t/s |
|
|
|
|
|
运动速度v/cm/s |
|
|
9 |
|
|
运动距离y/cm |
|
|
19 |
|
|
小聪探究发现,黑球的运动速度 与运动时间 之间成一次函数关系,运动距离 与运动时间 之间成二次函数关系.
(1)直接写出 关于 的函数解析式和 关于 的函数解析式(不要求写出自变量的取值范围);
(2)当黑球减速后运动距离为 时,求它此时的运动速度;
(3)若白球一直以 的速度匀速运动,问黑球在运动过程中会不会碰到白球?请说明理由.
计算:( -
- )×
)×
如图1,在平面直角坐标系中,A(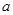 ,0),B(0,
,0),B(0,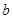 ),且
),且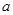 、
、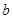 满足
满足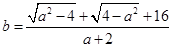 .
.
(1)求直线AB的解析式;
(2)若点M为直线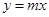 在第一象限上一点,且△ABM是等腰直角三角形,求
在第一象限上一点,且△ABM是等腰直角三角形,求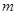 的值.
的值.
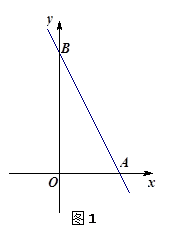
(3)如图3过点A的直线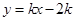 交
交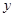 轴负半轴于点P,N点的横坐标为-1,过N点的直线
轴负半轴于点P,N点的横坐标为-1,过N点的直线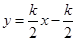 交AP于点M,给出两个结论:①
交AP于点M,给出两个结论:①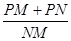 的值是不变;②
的值是不变;②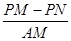 的值是不变,只有一个结论是正确,请你判断出正确的结论,并加以证明和求出其值。
的值是不变,只有一个结论是正确,请你判断出正确的结论,并加以证明和求出其值。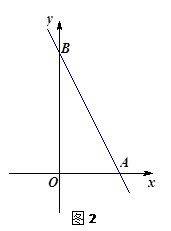
已知△ABC是等边三角形,点P是AC上一点,PE⊥BC于点E,交AB于点F,在CB的延长线上截取BD=PA,PD交AB于点I,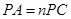 .
.
(1)如图1,若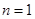 ,则
,则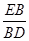 = ,
= ,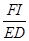 = ;
= ;
(2)如图2,若∠EPD=60º,试求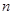 和
和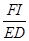 的值;
的值;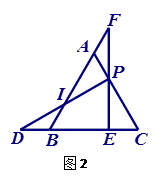
(3)如图3,若点P在AC边的延长线上,且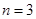 ,其他条件不变,则
,其他条件不变,则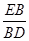 = .(只写答案不写过程)
= .(只写答案不写过程)
某公司有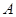 型产品40件,
型产品40件,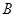 型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表:
型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表:
 型利润 型利润 |
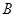 型利润 型利润 |
|
| 甲店 |
200 |
170 |
| 乙店 |
160 |
150 |
(1)设分配给甲店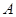 型产品
型产品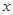 件,这家公司卖出这100件产品的总利润为
件,这家公司卖出这100件产品的总利润为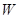 (元),求
(元),求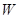 关于
关于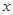 的函数关系式,并求出
的函数关系式,并求出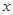 的取值范围;
的取值范围;
(2)若公司要求总利润不低于17560元,有多少种不同分配方案,哪种方案总利润最大,并求出最大值。
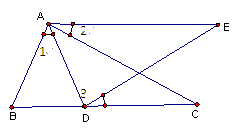
如图所示,已知△ABC中,点D为BC边上一点,∠1=∠2=∠3,AC=AE,
(1)求证:△ABC≌△ADE
(2)若AE∥BC,且∠E= 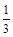 ∠CAD,求∠C的度数。
∠CAD,求∠C的度数。