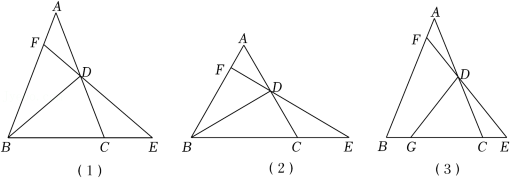
【问题提出】
如图(1),在 中, , 是 的中点,延长 至点 ,使 ,延长 交 于点 ,探究 的值.
【问题探究】
(1)先将问题特殊化.如图(2),当 时,直接写出 的值;
(2)再探究一般情形.如图(1),证明(1)中的结论仍然成立.
【问题拓展】
如图(3),在 中, , 是 的中点, 是边 上一点, ,延长 至点 ,使 ,延长 交 于点 .直接写出 的值(用含 的式子表示).
如图,DE∥BC,EF∥CG,AD:AB=1:3,AE=3.
(1)求EC的值;
(2)求证:AD•AG=AF•AB.
解方程:
(1)x(x-2)=x-2;
(2)(x+8)(x+1)=-12.
如图,抛物线y=ax2+bx+c经过原点,与x轴相交于点E(8,0),抛物线的顶点A在第四象限,点A到x轴的距离AB=4,点P(m,0)在线段OB上,连结PA,将线段PA绕点P逆时针旋转90°得到线段PC,过点C作y轴的平行线交x轴于点G,交抛物线于点D,连结BC和AD.
(1)求抛物线的解析式;
(2)求点C的坐标(用含m的代数式表示);
(3)当四边形ABCD是平行四边形时,求点P的坐标.
如图①,已知四边形ABCD是正方形,点E是AB的中点,点F在边CB的延长线上,且BE=BF,连接EF.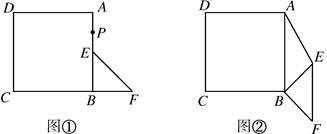
(1)若取AE的中点P,求证: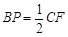 ;
;
(2)在图①中,若将△BEF绕点B顺时针方向旋转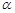 (
(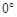 <
<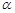 <
<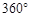 ),如图②,是否存在某位置,使得AE∥BF,若存在,求出所有可能的旋转角
),如图②,是否存在某位置,使得AE∥BF,若存在,求出所有可能的旋转角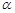 的大小;若不存在,请说明理由;
的大小;若不存在,请说明理由;
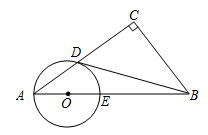
已知:如图所示,在Rt△ABC中,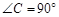 ,点O在AB上,以O为圆心,OA长为半径的圆与AC,AB分别交于点D,E,且
,点O在AB上,以O为圆心,OA长为半径的圆与AC,AB分别交于点D,E,且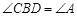 .判断直线BD与⊙O的位置关系,并证明你的结论.
.判断直线BD与⊙O的位置关系,并证明你的结论.