如图①，已知四边形ABCD是正方形，点E是AB的中点，点F在-优题课

如图①，已知四边形ABCD是正方形，点E是AB的中点，点F在边CB的延长线上，且BE=BF，连接EF．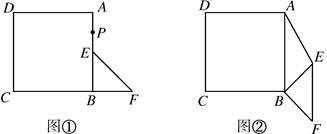

（1）若取AE的中点P，求证：；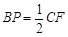
（2）在图①中，若将△BEF绕点B顺时针方向旋转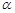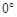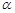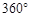（＜＜），如图②，是否存在某位置，使得AE∥BF，若存在，求出所有可能的旋转角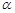的大小；若不存在，请说明理由；

科目数学题型解答题难度较难

知识点：对称式和轮换对称式

中央电视台的"中国诗词大赛"节目文化品位高，内容丰富．某校初二年级模拟开展"中国诗词大赛"比赛，对全年级同学成绩进行统计后分为"优秀"、"良好"、"一般"、"较差"四个等级，并根据成绩绘制成如下两幅不完整的统计图，请结合统计图中的信息，回答下列问题：

（1）扇形统计图中"优秀"所对应扇形的圆心角为　　度，并将条形统计图补充完整．

（2）此次比赛有四名同学获得满分，分别是甲、乙、丙、丁，现从这四名同学中挑选两名同学参加学校举行的"中国诗词大赛"比赛，请用列表法或画树状图法，求出选中的两名同学恰好是甲、丁的概率．

如图，直线 $EF / / GH$ ，点 $A$ 在 $EF$ 上， $AC$ 交 $GH$ 于点 $B$ ，若 $∠ FAC = 72 °$ ， $∠ ACD = 58 °$ ，点 $D$ 在 $GH$ 上，求 $∠ BDC$ 的度数．

如图，在平面直角坐标系中，抛物线 $y = \frac{\sqrt{3}}{3} x^{2} - \frac{2 \sqrt{3}}{3} x - \sqrt{3}$ 与 $x$ 轴交于 $A$ 、 $B$ 两点（点 $A$ 在点 $B$ 的左侧），与 $y$ 轴交于点 $C$ ，对称轴与 $x$ 轴交于点 $D$ ，点 $E (4, n)$ 在抛物线上．

（1）求直线 $AE$ 的解析式；

（2）点 $P$ 为直线 $CE$ 下方抛物线上的一点，连接 $PC$ ， $PE$ ．当 $ΔPCE$ 的面积最大时，连接 $CD$ ， $CB$ ，点 $K$ 是线段 $CB$ 的中点，点 $M$ 是 $CP$ 上的一点，点 $N$ 是 $CD$ 上的一点，求 $KM + MN + NK$ 的最小值；

（3）点 $G$ 是线段 $CE$ 的中点，将抛物线 $y = \frac{\sqrt{3}}{3} x^{2} - \frac{2 \sqrt{3}}{3} x - \sqrt{3}$ 沿 $x$ 轴正方向平移得到新抛物线 $y'$ ， $y'$ 经过点 $D$ ， $y'$ 的顶点为点 $F$ ．在新抛物线 $y'$ 的对称轴上，是否存在点 $Q$ ，使得 $ΔFGQ$ 为等腰三角形？若存在，直接写出点 $Q$ 的坐标；若不存在，请说明理由．

对任意一个三位数 $n$ ，如果 $n$ 满足各数位上的数字互不相同，且都不为零，那么称这个数为“相异数”．将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数，把这三个新三位数的和与111的商记为 $F (n)$ ．例如 $n = 123$ ，对调百位与十位上的数字得到213，对调百位与个位上的数字得到321，对调十位与个位上的数字得到132，这三个新三位数的和为 $213 + 321 + 132 = 666$ ， $666 \div 111 = 6$ ，所以 $F (123) = 6$ ．

（1）计算： $F (243)$ ， $F (617)$ ；

（2）若 $s$ ， $t$ 都是“相异数”，其中 $s = 100 x + 32$ ， $t = 150 + y (1 ⩽ x ⩽ 9$ ， $1 ⩽ y ⩽ 9$ ， $x$ ， $y$ 都是正整数），规定： $k = \frac{F (s)}{F (t)}$ ，当 $F (s) + F (t) = 18$ 时，求 $k$ 的最大值．

在 $ΔABM$ 中， $∠ ABM = 45 °$ ， $AM ⊥ BM$ ，垂足为 $M$ ，点 $C$ 是 $BM$ 延长线上一点，连接 $AC$ ．

（1）如图1，若 $AB = 3 \sqrt{2}$ ， $BC = 5$ ，求 $AC$ 的长；

（2）如图2，点 $D$ 是线段 $AM$ 上一点， $MD = MC$ ，点 $E$ 是 $ΔABC$ 外一点， $EC = AC$ ，连接 $ED$ 并延长交 $BC$ 于点 $F$ ，且点 $F$ 是线段 $BC$ 的中点，求证： $∠ BDF = ∠ CEF$ ．

试卷网试题网古诗词网作文网范文网