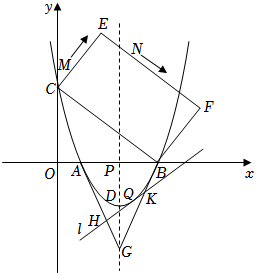
如图,已知抛物线 与 轴交于 两点,与 轴交于点 ,点 为抛物线的顶点.
(1)求抛物线的函数表达式及点 的坐标;
(2)若四边形 为矩形, .点 以每秒 个单位的速度从点 沿 向点 运动,同时点 以每秒 个单位的速度从点 沿 向点 运动,一点到达终点,另一点随之停止.当以 为顶点的三角形与 相似时,求运动时间 的值;
(3)抛物线的对称轴与 轴交于点 ,点 是点 关于点 的对称点,点 是 轴下方抛物线上的动点.若过点 的直线 与抛物线只有一个公共点,且分别与线段 相交于点 ,求证: 为定值.
如图,AC是⊙O的直径,OB是⊙O的半径,PA切⊙O于点A,PB与AC的延长线交于点M,∠COB=∠APB.
(1)求证:PB是⊙O的切线;
(2)当OB=3,PA=6时,求MB,MC的长.
如图,▱ABCD放置在平面直角坐标系中,已知点A(2,0),B(6,0),D(0,3),反比例函数的图象经过点C.
(1)求反比例函数的解析式;
(2)将▱ABCD向上平移,使点B恰好落在双曲线上,此时A,B,C,D的对应点分别为A′,B′,C′,D′,且C′D′与双曲线交于点E,求线段AA′的长及点E的坐标.
已知关于x的一元二次方程 .
.
(1)若方程有实数根,求实数m的取值范围;
(2)若方程两实数根为 ,
, ,且满足
,且满足 ,求实数
,求实数 的值.
的值.
热气球的探测器显示,从热气球底部A处看一栋高楼顶部的俯角为30°,看这栋楼底部的俯角为60°,热气球A处于地面距离为420米,求这栋楼的高度.
某校男子足球队的年龄分布如下面的条形图所示.
(1)求这些队员的平均年龄;
(2)下周的一场校际足球友谊赛中,该校男子足球队将会有11名队员作为首发队员出场,不考虑其他因素,请你求出其中某位队员首发出场的概率.