综合与实践
问题情境:我国东周到汉代一些出土实物上反映出一些几何作图方法,如侯马铸铜遗址出土车軎(wèi)范、芯组成的铸型(如图1),它的端面是圆形.如图2是用“矩”(带直角的角尺)确定端面圆心的方法:将“矩”的直角尖端A沿圆周移动,直到 ,在圆上标记 三点;将“矩”向右旋转,使它左侧边落在 点上,“矩”的另一条边与的交点标记为 点,这样就用“矩”确定了圆上等距离的 四点,连接 相交于点 ,即 为圆心.

问题解决:(1)请你根据“问题情境”中提供的方法,用三角板还原我国古代几何作图确定圆心 .如图3,点 在 上, ,且 ,请作出圆心 .(保留作图痕迹,不写作法)
类比迁移:(2)小梅受此问题的启发,在研究了用“矩”(带直角的角尺)确定端面圆心的方法后发现,如果 和 不相等,用三角板也可以确定圆心 .如图4,点 在 上, ,请作出圆心 .(保留作图痕迹,不写作法)
拓展探究:(3)小梅进一步研究,发现古代由“矩”度量确定圆上等距离点时存在误差,用平时学的尺规作图的方法确定圆心可以减少误差.如图5,点 是 上任意三点,请用不带刻度的直尺和圆规作出圆心 .(保留作图痕迹,不写作法)请写出你确定圆心的理由:________________.
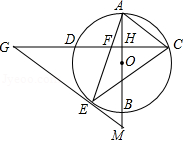
如图, 是 的直径,弦 ,垂足为 ,连接 ,过 上一点 作 交 的延长线于点 ,连接 交 于点 ,且 ,连接 .
(1)求证: ;
(2)求证: 是 的切线;
(3)延长 交 的延长线于点 ,若 , ,求 的值.
为响应国家全民阅读的号召,某社区鼓励居民到社区阅览室借阅读书,并统计每年的借阅人数和图书借阅总量(单位:本).该阅览室在2014年图书借阅总量是7500本,2016年图书借阅总量是10800本.
(1)求该社区的图书借阅总量从2014年至2016年的年平均增长率;
(2)已知2016年该社区居民借阅图书人数有1350人,预计2017年达到1440人.如果2016年至2017年图书借阅总量的增长率不低于2014年至2016年的年平均增长率,那么2017年的人均借阅量比2016年增长 ,求 的值至少是多少?
为调查广西北部湾四市市民上班时最常用的交通工具的情况,随机抽取了四市部分市民进行调查,要求被调查者从“ :自行车, :电动车, :公交车, :家庭汽车, :其他”五个选项中选择最常用的一项,将所有调查结果整理后绘制成如下不完整的条形统计图和扇形统计图,请结合统计图回答下列问题:

(1)在这次调查中,一共调查了 名市民,扇形统计图中, 组对应的扇形圆心角是 ;
(2)请补全条形统计图;
(3)若甲、乙两人上班时从 、 、 、 四种交通工具中随机选择一种,则甲、乙两人恰好选择同一种交通工具上班的概率是多少?请用画树状图或列表法求解.
如图,矩形 的对角线 , 相交于点 ,点 , 在 上, .
(1)求证: ;
(2)若 , ,求矩形 的面积.

如图,在平面直角坐标系中, 的三个顶点分别为 , , .
(1)把 向上平移3个单位后得到△ ,请画出△ 并写出点 的坐标;
(2)已知点 与点 关于直线 成轴对称,请画出直线 及 关于直线 对称的△ ,并直接写出直线 的函数解析式.
