综合与实践
【问题情境】数学活动课上，老师带领同学们开展“利用树叶的特征对树木进行分类”的实践活动．
【实践发现】同学们随机收集芒果树、荔枝树的树叶各10片，通过测量得到这些树叶的长y（单位：cm），宽x（单位：cm）的数据后，分别计算长宽比，整理数据如下：
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
芒果树叶的长宽比 |
3.8 |
3.7 |
3.5 |
3.4 |
3.8 |
4.0 |
3.6 |
4.0 |
3.6 |
4.0 |
荔枝树叶的长宽比 |
2.0 |
2.0 |
2.0 |
2.4 |
1.8 |
1.9 |
1.8 |
2.0 |
1.3 |
1.9 |
【实践探究】分析数据如下：
平均数 |
中位数 |
众数 |
方差 |
|
芒果树叶的长宽比 |
3.74 |
m |
4.0 |
0.0424 |
荔枝树叶的长宽比 |
1.91 |
1.95 |
n |
0.0669 |
【问题解决】
（1）上述表格中：m＝ ，n＝ ；
（2）①A同学说：“从树叶的长宽比的方差来看，我认为芒果树叶的形状差别大．”
②B同学说：“从树叶的长宽比的平均数、中位数和众数来看，我发现荔枝树叶的长约为宽的两倍．”
上面两位同学的说法中，合理的是 （填序号）；
（3）现有一片长11cm，宽5.6cm的树叶，请判断这片树叶更可能来自于芒果、荔枝中的哪种树？并给出你的理由．
如图，已知抛物线
与x轴交于点A，与y轴交于点B，动点Q从点O出发，以每秒2个单位长度的速度在线段OA上运动，过点Q作x轴的垂线交线段AB于点N，交抛物线于点P，设运动的时间为t秒。
问：△AON能否为等腰三角形？若能，求出t的值；若不能，请说明理由。
如图，在直角梯形ABCD中,AD∥CB, 
,动点P从点D出发,沿射线DA的方向以每秒2个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒一个单位长的速度向点B运动,点P,Q分别从点D,C同时出发,当点Q运动到点B时,点P随之停止运动.设运动的时间为t（秒）.
（1）设△BPQ的面积为S,求S与t之间的函数关系式;
（2）当t为何值时,四边形ABQP是平行四边形.
（3）当t为何值时,以B,P,Q三点为顶点的三角形是等腰三角形?
如图，已知直角梯形ABCD中，AD∥BC，AB⊥BC，AD＝2，AB＝8，CD＝10．
（1）求梯形ABCD的面积；
（2）动点P从点B出发，以2个单位/s的速度沿B→A→D→C方向向点C运动；动点Q从点C出发，以2个单位/s的速度沿C→D→A方向向点A运动；过点Q作QE⊥BC于点E．若P、Q两点同时出发，当其中一点到达终点时另一点也随之停止运动，设运动时间为t秒．问：
①当点P在B→A上运动时，是否存在这样的t，使得直线PQ将梯形ABCD的周长平分？若存在，请求出t的值，并判断此时PQ是否平分梯形ABCD的面积；若不存在，请说明理由．
②在运动过程中，是否存在这样的t，使得以P、D、Q为顶点的三角形恰好是以DQ为一腰的等腰三角形？若存在，请求出所有符合条件的t的值；若不存在，请说明理由．
如图，在矩形ABCD中，AB＝12cm，BC＝8cm．点E、F、G分别从点A、B、C同时出发，沿矩形的边按逆时针方向移动，点E、G的速度均为2cm/s，点F的速度为4cm/s，当点F追上点G（即点F与点G重合）时，三个点随之停止移动．设移动开始后第ts时，△EFG的面积为Scm2。
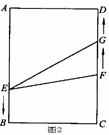
（1）当
＝1s时，S的值是多少？
（2）当
时，点E、F、G分别在边AB、BC、CD上移动，用含t的代数式表示S；当
时，点E在边AB上移动，点F、G都在边CD上移动，用含t的代数式表示S.
（3）若点F在矩形的边BC上移动，当为何值时，以点B、E、F为顶点的三角形与以C、F、G为顶点的三角形相似？请说明理由
如图所示，直线l：y=3x+3与x轴交于点A，与y轴交于点B．把△AOB沿y轴翻折，点A落到点C，抛物线过点B、C和D（3，0）．
（1）求直线BD和抛物线的解析式．
（2）若BD与抛物线的对称轴交于点M，点N在坐标轴上，以点N、B、D为顶点的三角形与△MCD相似，求所有满足条件的点N的坐标．
（3）在抛物线上是否存在点P，使S△PBD=6？若存在，求出点P的坐标；若不存在，说明理由．