在平面直角坐标系中，抛物线 （b是常数）经过点（2，0）．点A在抛物线上，且点A的横坐标为m（m≠0）．以点A为中心，构造正方形PQMN，PQ＝2|m|，且PQ⊥x轴．
（1）求该抛物线对应的函数表达式；
（2）若点B是抛物线上一点，且在抛物线对称轴左侧．过点B作x轴的平行线交抛物线于另一点C，连结BC．当BC＝4时，求点B的坐标；
（3）若m＞0，当抛物线在正方形内部的点的纵坐标y随x的增大而增大时，或者y随x的增大而减小时，求m的取值范围；
（4）当抛物线与正方形PQMN的边只有2个交点，且交点的纵坐标之差为 时，直接写出m的值．
如图，∠1=∠2，AB=AD，∠B=∠D，∠3=60º，请判断△AEC的形状，并说明理由。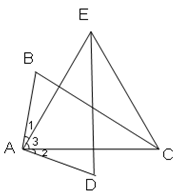
如图，在△ABC中，AB=AC，BD⊥AC，CE⊥AB，O是BD与CE的交点，求证：BO=OC．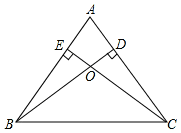
如图，折叠矩形纸片ABCD，先折出折痕（对角线）BD，再折叠AD边与对角线BD重合，得折痕DG，如图所示，若AB=8，BC=6，求AG的长．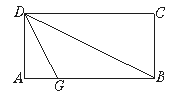
将纸片△ABC沿DE折叠使点A落在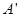
处的位置．
（1）如果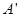落在四边形BCDE的内部（如图1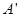），∠与∠1＋∠2之间存在怎样的数量关系？并说明理由．
（2）如果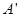落在四边形BCDE的的BE边上，这时图1中的∠1变为0°角，则∠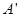与∠2之间的关系是．
（3）如果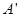落在四边形BCDE的外部（如图2），这时∠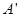与∠1、∠2之间又存在怎样的数量关系？并说明理由．（5+2+5=12分）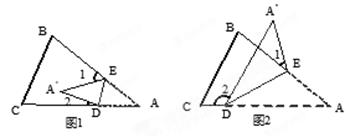
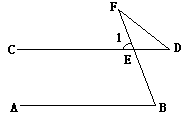
如图，AB∥CD，∠B = 78°，∠D = 32°，求∠F的度数．