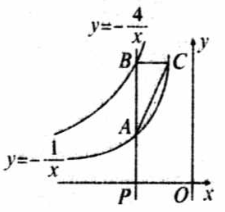
如图,点 为 轴负半轴上的一个点,过点 作 轴的垂线,交函数 的图象于点 ,交函数 的图象于点 ,过点 作 轴的平行线,交 于点 ,连接 .
(1)当点 的坐标为 时,求 的面积;
(2)若 ,求点 的坐标;
(3)连接 和 .当点 的坐标为 时, 的面积是否随 的值的变化而变化?请说明理由.
如图,已知:直线 交x轴于点A,交y轴于点B,抛物线y=ax2+bx+c经过A、B、C(1,0)三点.
交x轴于点A,交y轴于点B,抛物线y=ax2+bx+c经过A、B、C(1,0)三点.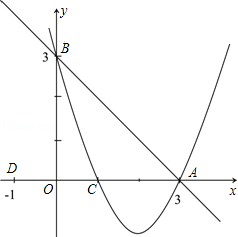
(1)求抛物线的解析式;
(2)若点D的坐标为(-1,0),在直线 上有一点P,使ΔABO与ΔADP相似,求出点P的坐标;
上有一点P,使ΔABO与ΔADP相似,求出点P的坐标;
(3)在(2)的条件下,在x轴下方的抛物线上,是否存在点E,使ΔADE的面积等于四边形APCE的面积?如果存在,请求出点E的坐标;如果不存在,请说明理由.
某商场计划购进一批甲、乙两种玩具,已知一件甲种玩具的进价与一件乙种玩具的进价的和为40元,用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同.
(1)求每件甲种、乙种玩具的进价分别是多少元?
(2)商场计划购进甲、乙两种玩具共48件,其中甲种玩具的件数少于乙种玩具的件数,商场决定此次进货的总资金不超过1000元,求商场共有几种进货方案?
如图,直角梯形ABCD中,AB∥DC,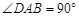 ,
, ,
,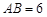 .动点M以每秒1个单位长的速度,从点A沿线段AB向点B运动;同时点P以相同的速度,从点C沿折线C-D-A向点A运动.当点M到达点B时,两点同时停止运动.过点M作直线l∥AD,与线段CD的交点为E,与折线A-C-B的交点为Q.点M运动的时间为t(秒).
.动点M以每秒1个单位长的速度,从点A沿线段AB向点B运动;同时点P以相同的速度,从点C沿折线C-D-A向点A运动.当点M到达点B时,两点同时停止运动.过点M作直线l∥AD,与线段CD的交点为E,与折线A-C-B的交点为Q.点M运动的时间为t(秒).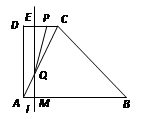
(1)当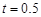 时,求线段
时,求线段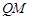 的长;
的长;
(2)当0<t<2时,如果以C、P、Q为顶点的三角形为直角三角形,求t的值;
(3)当t>2时,连接PQ交线段AC于点R.请探究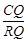 是否为定值,若是,试求这个定值;若不是,请说明理由.
是否为定值,若是,试求这个定值;若不是,请说明理由.
如图,正方形ABCD,点E、F分别为BC、CD边上的点,连接EF,点 M为EF上一点,且使AE平分∠BAM,AF平分∠DAM,证明:∠EAF=45°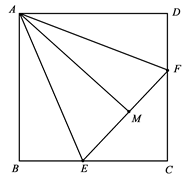
一张长方形的餐桌可以坐6个人,按照下图的方式摆放餐桌和椅子:
(1)观察表中数据规律填表:
| 餐桌张数 |
1 |
2 |
3 |
4 |
… n |
| 可坐人数 |
6 |
8 |
10 |
(2)一家酒楼,按上图的方式拼桌,要使拼成的一张大餐桌刚好能坐160人,请问需几张餐桌拼成一张大餐桌?
(3)若酒店有240人来一起就餐,要拼成一张大餐桌,怎样拼桌需要的餐桌最少?最少要用多少张?