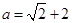某商场计划采购甲、乙、丙三种型号的“格力”牌空调共 台.三种型号的空调进价和售价如下表:

商场计划投入总资金 万元,所购进的甲、丙型号空调数量相同,乙型号数量不超过甲型号数量的一半,若设购买甲型号空调 台,所有型号空调全部售出后获得的总利润为 元.
(1)求 与 之间的函数关系式;
(2)商场如何采购空调才能获得最大利润
(3)由于原材料上涨,商场决定将丙型号空调的售价提高 元( ),其余型号售价不变,则商场又该如何采购才能获得最大利润?
若一次函数 (
( 是常数)与
是常数)与 (
( 是常数),满足
是常数),满足 且
且 ,则称这两函数是对称函数
,则称这两函数是对称函数当函数
 与
与 是对称函数,求
是对称函数,求 和
和 的值;
的值;在平面直角坐标系中,一次函数
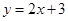 图象与
图象与 轴交于点
轴交于点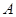 、与
、与 轴交于点
轴交于点 ,点
,点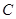 与点
与点 关于x轴对称,过点
关于x轴对称,过点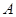 、
、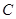 的直线解析式是
的直线解析式是 ,求证:函数
,求证:函数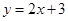 与
与 是对称函数
是对称函数
如图,在平行四边形 中,
中, ,延长
,延长 到
到 ,使
,使 ,过
,过 作
作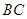 的垂线,交
的垂线,交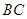 延长线于点
延长线于点 .
.
求证: .
.
欢欢有红色、白色、黄色三件上衣,又有米色、白色的两条裤子.她随机拿出一件上衣和一条裤子,用树状图(或列表法)表示所有可能出现的结果;
如果欢欢最喜欢的穿着搭配是白色上衣配米色裤子,求欢欢随机拿出一件上衣和一条裤子正好是她最喜欢的穿着搭配的概率.
如图,在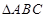 中,
中,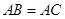 ,
, 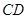 ⊥
⊥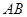 ,垂足为
,垂足为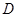 ,且
,且 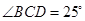 .求∠A的大小.
.求∠A的大小.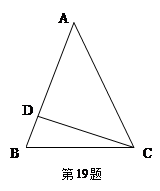
计算:
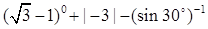
已知:
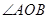 求作:
求作: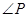 ,使得
,使得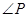
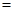
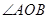 (尺规作图,不写作法,保留作图痕迹).
(尺规作图,不写作法,保留作图痕迹).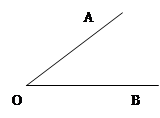
先化简,再求值:
 ,其中
,其中