我国是水资源比较贫乏的国家之一,各地采用了价格调控等手段来达到节约用水的目的.某市用水收费的方法是:水费 基本费十超额费十定额损耗费.若每月用水量不超过最低限量 时,只付基本费 元和每月的定额损耗费 元;若用水量超过 时,除了付同上的基本费和定额损耗费外,超过部分每立方米付 元的超额费.已知每户每月的定额损耗费不超过 元.
(1)当月用水量为 时,支付费用为 元,写出 关于 的函数关系式;
(2)该市一家庭今年一季度的用水量和支付费用见下表,根据表中数据求 .

列方程或方程组解应用题:
小明将一根长1.4米的细绳剪成3段,第一次剪下一段,第二次剪下的细绳比第一次剪下的细绳长0.2米,剩余的细绳长恰好是第一次剪下的细绳长的2倍,请问他剪下的三段细绳拉直后首尾顺次相接能否围成一个三角形?
如图,直线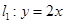 与直线
与直线 在同一平面直角坐标系内交于点P,且直线
在同一平面直角坐标系内交于点P,且直线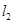 与x轴交于点A. 求直线
与x轴交于点A. 求直线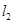 的解析式及△OAP的面积.
的解析式及△OAP的面积.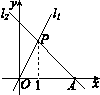
已知:如图,AC=AD,AB是∠CAD的角平分线.求证:BC=BD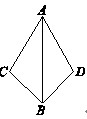
如图,已知二次函数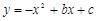 的图象经过A(
的图象经过A(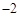 ,
,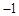 ),B(0,7)两点.
),B(0,7)两点.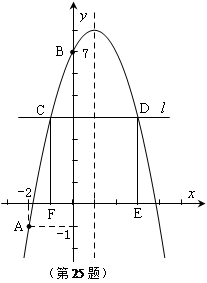
⑴求该抛物线的解析式及对称轴;
⑵当 为何值时,
为何值时,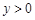 ?
?
⑶在 轴上方作平行于
轴上方作平行于 轴的直线
轴的直线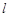 ,与抛物线交于C,D两点(点C在对称轴的左侧),过点C,D作
,与抛物线交于C,D两点(点C在对称轴的左侧),过点C,D作 轴的垂线,垂足分别为F,E.当矩形CDEF为正方形时,求C点的坐标.
轴的垂线,垂足分别为F,E.当矩形CDEF为正方形时,求C点的坐标.
如图,Rt△ABO的顶点A是双曲线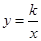 与直线
与直线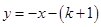 在第二象限的交点,AB⊥
在第二象限的交点,AB⊥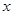 轴于B且S△ABO=
轴于B且S△ABO=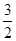 .
.
(1)求这两个函数的解析式;
(2)求直线与双曲线的两个交点A,C的坐标和△AOC的面积。