墨西哥爆发的甲型 流感疫情牵动着全世界人民的心,某医疗单位决定:紧急调拨由甲、乙、丙三种药品混合配制的防疫药品共 支援灾区.根据要求混合配制的防疫药品中至少需要含抗生素 个单位和抗菌素 个单位,且三种药品含抗生素和抗菌素的含量如下表:

并且甲、乙、丙三种药品所需成本分别为 万元 , 万元 和 万元 .设所取甲、乙、丙三种药品的质量分别为 .
(1)试问配制 这种防疫药品至少需要乙种药品多少千克?
(2)试用含 的式子表示配制 防疫药品的总成本 ?
(3)若限定配制后的药品中甲种药品的质量为 ,试求此时总成本 取最小值时,所取乙、丙两种药品的质量,并求出 的最小值.
如图,一轮船由B处向C处航行,在B处测得C处在B的北偏东75°方向上,在海岛上的观察所A测得B在A的南偏西30°方向上,C在A的南偏东25°方向。若轮船行驶到C处,那么从C处看A,B两处的视角∠ACB是多少度? 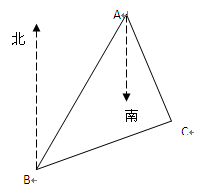
如图,EF∥AD,∠1=∠2, ∠BAC=70°,将求∠AGD的过程填空完整。
解:∵EF∥AD
∴∠2=()
又∵∠1=∠2
∴∠1=∠3()
∴AB∥()
∵∠BAC+=180°()
∵∠BAC=70°∴∠AGD=。
如图所示,已知BD平分∠ABC,∠C=62°,∠ABD=30°,∠ADC=118°,
求∠A的度数。
已知实数x,y满足y= +
+  —28,求
—28,求
如图,抛物线y=ax2+bx+2交x轴于A(﹣1,0),B(4,0)两点,交y轴于点C,与过点C且平行于x轴的直线交于另一点D,点P是抛物线上一动点.
(1)求抛物线解析式及点D坐标;
(2)点E在x轴上,若以A,E,D,P为顶点的四边形是平行四边形,求此时点P的坐标;
(3)过点P作直线CD的垂线,垂足为Q,若将△CPQ沿CP翻折,点Q的对应点为Q′.是否存在点P,使Q′恰好落在x轴上?若存在,求出此时点P的坐标;若不存在,说明理由.