如图,在锐角△ABC中, ,点D,E分别是边AB,AC上一动点,连接BE交直线CD于点F.
(1)如图1,若 ,且 , ,求 的度数;
(2)如图2,若 ,且 ,在平面内将线段AC绕点C顺时针方向旋转60°得到线段CM,连接MF,点N是MF的中点,连接CN.在点D,E运动过程中,猜想线段BF,CF,CN之间存在的数量关系,并证明你的猜想;
(3)若 ,且 ,将 沿直线AB翻折至 所在平面内得到 ,点H是AP的中点,点K是线段PF上一点,将 沿直线HK翻折至 所在平面内得到 ,连接PQ.在点D,E运动过程中,当线段PF取得最小值,且 时,请直接写出 的值.

某学校组织340名师生进行长途考察活动,带有行李170件,计划租用甲、乙两种型号的汽车共10辆.经了解,甲车每辆最多能载40人和16件行李,乙车每辆最多能载30人和20件行李.
(1)请你帮助学校设计所有可行的租车方案.
(2)如果甲车的租金为每辆2 000元,乙车的租金为每辆1 800元,问哪种可行方案使租车费用最省?
某电脑经销商计划同时购进一批电脑机箱和液晶显示器,若购进电脑机箱10台和液晶显示器8台,共需要资金7 000元;若购进电脑机箱2台和液晶显示器5台,共需要资金4 120元.每台电脑机箱、液晶显示器的进价各是多少元?
已知2a-1的平方根是±3,3a+b-1的算术平方根是4,求a+2b的值.
2012年我市某县筹备20周年县庆,园林部门决定利用现有的3 490盆甲种花卉和2 950盆乙种花卉搭配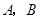 两种园艺造型共50个摆放在迎宾大道两侧,已知搭配一个
两种园艺造型共50个摆放在迎宾大道两侧,已知搭配一个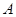 种造型需甲种花卉80盆,乙种花卉40盆,搭配一个
种造型需甲种花卉80盆,乙种花卉40盆,搭配一个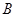 种造型需甲种花卉50盆,乙种花卉90盆.
种造型需甲种花卉50盆,乙种花卉90盆.
(1)某校九年级(1)班课外活动小组承接了这个园艺造型搭配方案的设计,问符合题意的搭配方案有几种?请你帮助设计出来.
(2)若搭配一个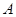 种造型的成本是800元,搭配一个
种造型的成本是800元,搭配一个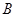 种造型的成本是960元,试说明(1)中哪种方案成本最低?最低成本是多少元?
种造型的成本是960元,试说明(1)中哪种方案成本最低?最低成本是多少元?
今秋,某市白玉村水果喜获丰收,果农王灿收获枇杷20吨,桃子12吨.现计划租用甲、乙两种货车共8辆将这批水果全部运往外地销售,已知一辆甲种货车可装枇杷4吨和桃子1吨,一辆乙种货车可装枇杷和桃子各2吨.
(1)王灿如何安排甲、乙两种货车可一次性地运到销售地?有几种方案?
(2)若甲种货车每辆要付运输费300元,乙种货车每辆要付运输费240元,则果农王灿应选择哪种方案,使运输费最少?最少运费是多少?