已知椭圆 的离心率为 ,点 在 上.
(1)求 的方程;
(2)过点 的直线交 于点 , 两点,直线 , 与 轴的交点分别为 , ,证明:线段 的中点为定点.
(本小题满分12分)
已知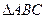 中,角
中,角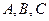 所对的边分别为
所对的边分别为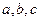 又
又 ,
, :
: =2:3.
=2:3.
(1)求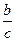 的值;(2)若
的值;(2)若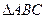 的边
的边 上的高为
上的高为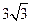 ,求a的值.
,求a的值.
(本小题满分12分)
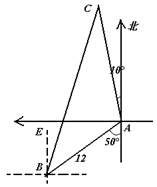
我缉私巡逻艇在一小岛A南偏西50º的方向,距小岛12海里的B处,发现隐藏在小岛边上的一走私船正开始向岛北偏西 10º方向行驶,测得其速度为每小时10海里,问我巡逻艇须用多大的速度朝什么方向航行才能恰在两小时后截获该走私船?(必要时,可参考下列数据sin38º≈0.62,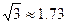 )
)
(本小题满分12分)
三个数成等比数列,其积为512,如果第一个数与第三个数各减2,则成等差数列,求这三个数.
(本小题满分10分)
某工厂第n年的生产总值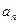 的信息如图所示:
的信息如图所示: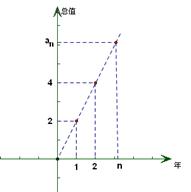
(1)写出 的值;(2)求
的值;(2)求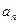 ;
;
(3)求前n年的生产总值 .
.
(本小题满分14分)
如图,在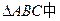 ,已知A(-
,已知A(- ,0), B(
,0), B( ,0), CD
,0), CD AB于D,
AB于D,  的垂心为H,且
的垂心为H,且
(Ⅰ)求点H的轨迹方程;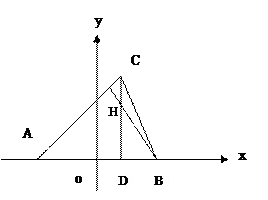
(Ⅱ)若过定点F(0,2)的直线交曲线 于不同的两点
于不同的两点 (点
(点 在F,H之间),且满足
在F,H之间),且满足 ,求
,求 的取值范围.
的取值范围.