五个人站成一排,求在下列条件下的不同排法种数:
(1)甲必须在排头;
(2)甲、乙相邻;
(3)甲不在排头,并且乙不在排尾;
(4)其中甲、乙两人自左向右从高到矮排列且互不相邻.
已知直线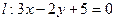 及定点P(3,-2)依下列条件求直线l1和l2的方程:
及定点P(3,-2)依下列条件求直线l1和l2的方程:
(1)l1过点P且l1// l;
(2)l2过点P且l2⊥l
如图所示,AB是圆O的直径,PA垂直于圆O所在平面,C是圆周上不同于A、B的任意一点,求证:平面PAC⊥平面PBC
设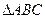 的外心为O,以线段OA、OB为邻边作平行四边形,第四个顶点为D,再以OC、OD为邻边作平行四边形,它的第四个顶点为H 。
的外心为O,以线段OA、OB为邻边作平行四边形,第四个顶点为D,再以OC、OD为邻边作平行四边形,它的第四个顶点为H 。
(1)若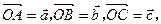 用
用 ;
;
(2)求证: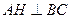 ;
;
(3)设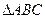 中,
中, 外接圆半径为R, 用
外接圆半径为R, 用
R表示 .(外心是三角形外接圆的圆心)
.(外心是三角形外接圆的圆心)
某地区有三座工厂分别位于△ABC的三个顶点,已知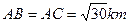 、
、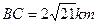 . 为了处理三个工厂的污水,现要在△ABC区域内(不包括边界)且与B、C等距的一点O处建立一个污水处理厂,并铺设排污管道OA、OB、OC.设
. 为了处理三个工厂的污水,现要在△ABC区域内(不包括边界)且与B、C等距的一点O处建立一个污水处理厂,并铺设排污管道OA、OB、OC.设 ,当排污管道总长取最小值时,求
,当排污管道总长取最小值时,求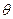 的值.
的值.
已知函数
(Ⅰ)设 为正常数,若
为正常数,若 在区间
在区间 上是增函数,求
上是增函数,求 的取值范围;
的取值范围;
(Ⅱ)设集合 ,若不等式
,若不等式 对于
对于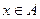 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。