已知复平面内平行四边形ABCD(A,B,C,D按逆时针排列),A点对应的复数为2+i,向量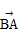 对应的复数为1+2i,向量
对应的复数为1+2i,向量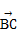 对应的复数为3-i.
对应的复数为3-i.
(1)求点C,D对应的复数.
(2)求平行四边形ABCD的面积.
已知向量 =
= ,
, =
= ,定义函数f(x)=
,定义函数f(x)= ·
· .
.
(1)求函数f(x)的表达式,并指出其最大值和最小值.
(2)在锐角△ABC中,角A,B,C的对边分别为a,b,c,且f(A)=1,bc=8,求△ABC的面积S.
在△ABC中,内角A,B,C的对边分别是a,b,c,且a2=b2+c2+ ab.
ab.
(1)求A.
(2)设a= ,S为△ABC的面积,求S+3cosBcosC的最大值,并指出此时B的值.
,S为△ABC的面积,求S+3cosBcosC的最大值,并指出此时B的值.
已知函数f(x)=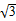 sinωxcosωx-cos2ωx,其中ω为使f(x)能在x=
sinωxcosωx-cos2ωx,其中ω为使f(x)能在x=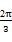 时取得最大值的最小正整数.
时取得最大值的最小正整数.
(1)求ω的值.
(2)设△ABC的三边长a,b,c满足b2=ac,且边b所对的角θ的取值集合为M,当x∈M时,求f(x)的值域.
如图,渔船甲位于岛屿A的南偏西60°方向的B处,且与岛屿A相距12海里,渔船乙以10海里/小时的速度从岛屿A出发沿正北方向航行,若渔船甲同时从B处出发沿北偏东α的方向追赶渔船乙,刚好用2小时追上.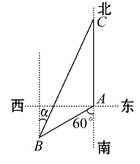
(1)求渔船甲的速度.
(2)求sinα的值.