对于平面直角坐标系xOy中的点P和线段AB,给出如下定义:在线段AB外有一点P,如果在线段AB上存在两点C、D,使得∠CPD=90°,那么就把点P叫做线段AB的悬垂点.
(1)已知点A(2,0),O(0,0)
①若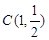 ,D(1,1),E(1,2),在点C,D,E中,线段AO的悬垂点是______;
,D(1,1),E(1,2),在点C,D,E中,线段AO的悬垂点是______;
②如果点P(m,n)在直线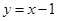 上,且是线段AO的悬垂点,求
上,且是线段AO的悬垂点,求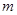 的取值范围;
的取值范围;
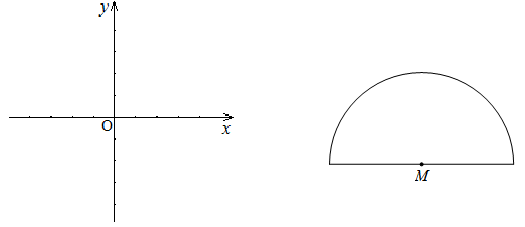
(2)如下图是帽形M(半圆与一条直径组成,点M是半圆的圆心),且圆M的半径
是1,若帽形内部的所有点是某一条线段的悬垂点,求此线段长的取值范围.
(本小题满分12分)
已知函数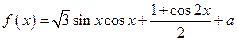 (
( 为常数).
为常数).
(1)求函数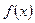 的最小正周期,并指出其单调减区间;
的最小正周期,并指出其单调减区间;
(2)若函数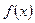 在
在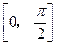 上的最大值是2,试求实数
上的最大值是2,试求实数 的值.
的值.
(本小题满分14分)已知函数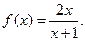
(1)当 时, 证明: 不等式
时, 证明: 不等式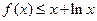 恒成立;
恒成立;
(2)若数列 满足
满足 ,证明数列
,证明数列 是等比数列,并求出数列
是等比数列,并求出数列 、
、 的通项公式;
的通项公式;
(3)在(2)的条件下,若 ,证明:
,证明: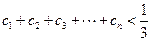 .
.
(本小题满分14分)已知函数 。
。
(1)当 时,求曲线
时,求曲线 在点
在点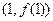 处的切线方程;
处的切线方程;
(2)求 的单调区间。
的单调区间。
(本小题满分14分) 已知中心在坐标原点 的椭圆
的椭圆 经过点
经过点 ,且点
,且点 为其右焦点。
为其右焦点。
(1)求椭圆 的方程;
的方程;
(2)是否存在平行于 的直线
的直线 ,使得直线
,使得直线 与椭圆
与椭圆 有公共点,且直线
有公共点,且直线 与
与 的距离等于4?若存在,求出直线
的距离等于4?若存在,求出直线 的方程;若不存在,请说明理由。
的方程;若不存在,请说明理由。
(本小题满分14分) 如图3所示,四棱锥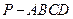 中,底面
中,底面 为正方形,
为正方形,  平面
平面 ,
, ,
,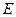 ,
, ,
, 分别为
分别为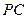 、
、 、
、 的中点.
的中点.
(1)求证: ;
;
(2)求二面角D-FG-E的余弦值. 