某单位为绿化环境,移栽了甲、乙两种大树各2株.设甲、乙两种大树移栽的成活率分别为
和
,且各株大树是否成活互不影响.求移栽的4株大树中:
(Ⅰ)两种大树各成活1株的概率;
(Ⅱ)成活的株数
的分布列与期望.
设数列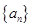 满足
满足
(I)求数列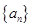 的通项公式;
的通项公式;
(II)设 求数列
求数列 的前
的前 项和
项和 .
.
在正项等比数列 中,
中, ,
,  .
.
(1) 求数列 的通项公式
的通项公式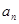 ;
;
(2) 记 ,求数列
,求数列 的前n项和
的前n项和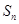 ;
;
(3) 记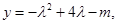 对于(2)中的
对于(2)中的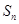 ,不等式
,不等式 对一切正整数n及任意实数
对一切正整数n及任意实数 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
如图,某动物园要建造两间完全相同的矩形熊猫居室,其总面积为24平方米,设熊猫居室的一面墙AD的长为x米  .
.
(1)用x表示墙AB的长;
(2)假设所建熊猫居室的墙壁造价(在墙壁高度一定的前提下)为每米1000元,请将墙壁的总造价y(元)表示为x(米)的函数;
(3)当x为何值时,墙壁的总造价最低?
如图,在四棱锥P-ABCD中,底面ABCD是正方形,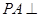 底面
底面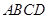 ,且PA=AB.
,且PA=AB.
(1)求证:BD 平面PAC;
平面PAC;
(2)求异面直线BC与PD所成的角.
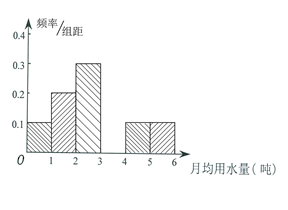
某市为节约用水,计划在本市试行居民生活用水定额管理,为了较为合理地确定居民日常用水量的标准,通过抽样获得了100位居民某年的月均用水量(单位:吨),右表是100位居民月均用水量的频率分布表,根据右表解答下列问题:
| 分组 |
频数 |
频率 |
| [0,1) |
10 |
0.10 |
| [1,2) |
 |
0.20 |
| [2,3) |
30 |
0.30 |
| [3,4) |
20 |
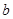 |
| [4,5) |
10 |
0.10 |
| [5,6] |
10 |
0.10 |
| 合计 |
100 |
1.00 |
(1)求右表中 和
和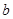 的值;
的值;
(2)请将频率分布直方图补充完整,并根据直方图估计该市每位居民月均用水量的众数.