(本小题满分14分)
设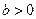 ,椭圆方程为
,椭圆方程为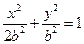 ,抛物线方程为
,抛物线方程为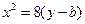 .如图6所示,过点
.如图6所示,过点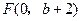 作
作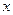 轴的平行线,与抛物线在第一象限的交点为
轴的平行线,与抛物线在第一象限的交点为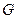 ,已知抛物线在点
,已知抛物线在点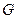 的切线经过椭圆的右焦点
的切线经过椭圆的右焦点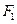 .
.
(1)求满足条件的椭圆方程和抛物线方程;
(2)设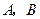 分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点
分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点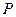 ,使得
,使得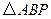 为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).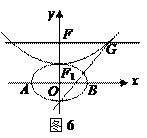
在△ABC中,已知B=45°,D是BC边上的一点,AB=5
 ,AC="14," DC=6,求AD的长.
,AC="14," DC=6,求AD的长.
本小题满分14分)
定义运算 ,记函数
,记函数
(Ⅰ)已知 ,且
,且 ,求
,求 的值;
的值;
(Ⅱ)在给定的直角坐标系中,用“五点法”作出函数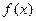 在
在
一个周期内的简图; (Ⅲ)求函数
(Ⅲ)求函数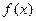 的对称中心、最大值及相应的
的对称中心、最大值及相应的 值.
值.
数列{an}满足Sn=2n-an,n∈N,先计算前4项后猜想an,并用数学归纳法证明
(本小题满分12分)
某公司近年来科研费用支出 万元与公司所获得利润
万元与公司所获得利润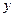 万元之间有如下的统计数据:
万元之间有如下的统计数据:
 |
2 |
3 |
4 |
5 |
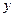 |
18 |
27 |
32 |
35 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出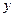 关于
关于 的线性回归方程
的线性回归方程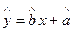 ;
;
(3)试根据(2)求出的线性回归方程,预测该公司科研费用支出为10万元时公司所获得的利润.
参考公式: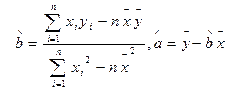
(本小题满分14分)
已知甲盒内有大小相同的1个红球和3个黑球,乙盒内有大小相同的2个红球和4个黑球。现从甲、乙两个盒内各任取2个球。
(1)求取出的4个球均为黑球的概率;
(2)求取出的4个球中恰有1个红球的概率;
(3)设 为取出的4个球中红球的个数,求
为取出的4个球中红球的个数,求 的分布列和数学期望
的分布列和数学期望