（本小题满分12分）如图，四棱锥P-ABCD中，PA⊥平面ABCD，PA＝AB＝BC＝2，E为PA的中点，过E作平行于底面的平面EFGH，分别与另外三条侧棱相交于点F、G、H. 已知底面ABCD为直角梯形，AD∥BC，AB⊥AD，∠BCD=135°.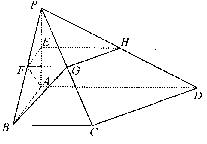
（1） 求异面直线AF与BG所成的角的大小；
（2） 求平面APB与平面CPD所成的锐二面角的大小.
已知复数
的实部为
，复数
的虚部为
，且
，
是实数，求复数和．
（本小题满分14分）已知函数
，
，且函数
与
的图象至多有一个公共点。
（Ⅰ）证明：当
时，
；
（Ⅱ）若不等式
对题设条件中的
总成立，求
的最小值．
（本小题满分15分）已知数列
中，
（实数
为常数），
，
是其前
项和，且
．数列
是等比数列，
，
恰为
与
的等比中项．
（Ⅰ）证明：数列是等差数列；
（Ⅱ）求数列
的通项公式；
（Ⅲ）若
，当
时
，
的前项和为
，求证：对任意
，都有
．
（本小题满分15分）已知椭圆C：
的离心率为
，左、右焦点分别为
，点
在椭圆C上，且
，
的面积为
．
（Ⅰ）求椭圆
的方程；
（Ⅱ）直线
与椭圆相交于
，
两点．点
，记直线
的斜率分别为
，当
最大时，求直线
的方程．
（本小题满分15分）已知四边形
中,
, 
为
中点，连接
，将
沿翻折到
,使得二面角
的平面角的大小为
．
（Ⅰ）证明:
；
（Ⅱ）已知二面角
的平面角的余弦值为
，求的大小及
的长．