(本小题满分14分)已知函数 ,
, ,且函数
,且函数 与
与 的图象至多有一个公共点。
的图象至多有一个公共点。
(Ⅰ)证明:当 时,
时, ;
;
(Ⅱ)若不等式 对题设条件中的
对题设条件中的 总成立,求
总成立,求 的最小值.
的最小值.
(本小题满分12分)
设函数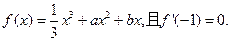
(1)试用含a的代数式表示b,
(2)求f(x)的单调区间;
(3)令a=-1,设函数f(x)在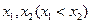 处取得极值,记点
处取得极值,记点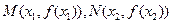 ,证明:线段MN与曲线f(x)存在异于M,N的公共点。
,证明:线段MN与曲线f(x)存在异于M,N的公共点。
(本小题满分12分)
已知椭圆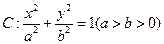 的离心率为
的离心率为 ,焦点到相应准线的距离为
,焦点到相应准线的距离为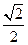
(1)求椭圆C的方程
(2)设直线 与椭圆C交于A、B两点,坐标原点到直线
与椭圆C交于A、B两点,坐标原点到直线 的距离为
的距离为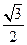 ,求
,求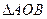 面积的最大值。
面积的最大值。
(本小题满分12分)
设 的前n项和,对
的前n项和,对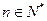 ,都有
,都有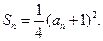
(1)求数列 的通项公式;
的通项公式;
(2)设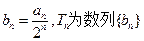 的前n项和,求证:
的前n项和,求证: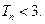
(本小题满分12分)
如图,四棱锥P—ABCD的底面ABCD是 边长为2的菱形,
边长为2的菱形,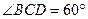 ,E是CD的中点,PA
,E是CD的中点,PA 底面ABC
底面ABC D,PA=4
D,PA=4
(1)证明:若F是棱PB的中点,求证:EF//平面PAD;
(2)求平面PAD和平面PBE所成二面角(锐角)的大小。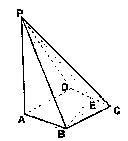
(本小题满分12分)
小明参加一次比赛,比赛共设三关。第一、二关各有两个问题,两个问题全答对,可进入下一关。第三关有三个问题,只要答对其中两个问题,则闯关成功。每过一关可一次性获得价值分别为100、300、500元的奖励。小明对三关中每个问题回答正确的概率依次为 且每个问题回答正确与否相互独立。
且每个问题回答正确与否相互独立。
(1)求小明过第一关但未过第二关的概率;
(2)求小明至少获得奖金400元的概率。