.(本小题满分12分)
在△ABC中,a,b,c分别是角A,B,C的对边,A为锐角,已知向量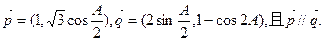
(1)若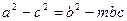 ,求实数m的值。
,求实数m的值。
(2)若 ,求△ABC面积的最大值.
,求△ABC面积的最大值.
 |
在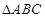 中,角A、B、C的对边分别为a、b、c,且角A、B、C成等差教列.(1)若
中,角A、B、C的对边分别为a、b、c,且角A、B、C成等差教列.(1)若 ,求边c的值;
,求边c的值;
(2)设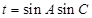 ,求t的最大值.
,求t的最大值.
已知数列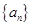 的首项
的首项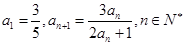 .
.
(1)求证:数列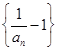 为等比数列;
为等比数列;
(2)记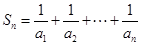 ,若
,若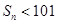 ,求最大正整数
,求最大正整数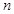 的值;
的值;
(3)是否存在互不相等的正整数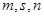 ,使
,使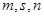 成等差数列,且
成等差数列,且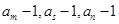 成等比数列?如果存在,请给予证明;如果不存在,请说明理由.
成等比数列?如果存在,请给予证明;如果不存在,请说明理由.
已知等差数列{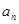 }的首项为
}的首项为 a
a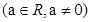 .设数列的前n项和为Sn,且对任意正整数n都有
.设数列的前n项和为Sn,且对任意正整数n都有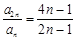 .
.
(1)求数列{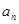 }的通项公式及Sn;
}的通项公式及Sn;
(2)是否存在正整数n和k,使得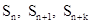 成等比数列?若存在,求出n和k的值;若不存在,请说明理由.
成等比数列?若存在,求出n和k的值;若不存在,请说明理由.
成等差数列的三个正数的和等于15,并且这三个数分别加上2、5、13后成为等比数列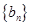 中的
中的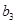 、
、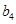 、
、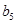 .
.
(1)求数列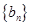 的通项公式;
的通项公式;
(2)数列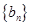 的前n项和为
的前n项和为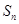 ,求证:数列
,求证:数列 是等比数列.
是等比数列.
已知向量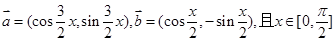 ,
,
(1)求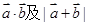 ;
;
(2)若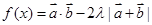 的最小值是
的最小值是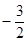 ,求实数
,求实数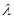 的值.
的值.