(本题满分14分)已知函数f(x)满足2ax·f(x)=2f(x)-1,f(1)=1,设无穷数列{an}满足an+1=f(an).(1)求函数f(x)的表达式;(2)若a1=3,从第几项起,数列{an}中的项满足an<an+1;(3)若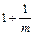 <a1<
<a1<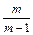 (m为常数且m∈N+,m≠1),求最小自然数N,使得当n≥N时,总有0<an<1成立。
(m为常数且m∈N+,m≠1),求最小自然数N,使得当n≥N时,总有0<an<1成立。
已知椭圆C: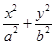 =1(a>b>0)上任一点P到两个焦点的距离的和为2
=1(a>b>0)上任一点P到两个焦点的距离的和为2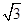 ,P与椭圆长轴两顶点连线的斜率之积为-
,P与椭圆长轴两顶点连线的斜率之积为-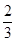 .设直线l过椭圆C的右焦点F,交椭圆C于两点A(x1,y1),B(x2,y2).
.设直线l过椭圆C的右焦点F,交椭圆C于两点A(x1,y1),B(x2,y2).
(1)若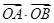 =
=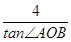 (O为坐标原点),求|y1-y2|的值;
(O为坐标原点),求|y1-y2|的值;
(2)当直线l与两坐标轴都不垂直时,在x轴上是否总存在点Q,使得直线QA,QB的倾斜角互为补角?若存在,求出点Q坐标;若不存在,请说明理由.
某创业投资公司拟投资开发某种新能源产品,估计能获得10万元到1 000万元的投资收益.现准备制定一个对科研课题组的奖励方案:资金y(单位:万元)随投资收益x(单位:万元)的增加而增加,且奖金不超过9万元,同时奖金不超过投资收益的20%.
(1)若建立函数y=f(x)模型制定奖励方案,试用数学语言表述该公司对奖励函数f(x)模型的基本要求,并分析函数y=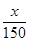 +2是否符合公司要求的奖励函数模型,并说明原因;
+2是否符合公司要求的奖励函数模型,并说明原因;
(2)若该公司采用模型函数y=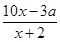 作为奖励函数模型,试确定最小的正整数a的值.
作为奖励函数模型,试确定最小的正整数a的值.
如图,在四棱锥PABCD中,PA⊥底面ABCD,AC⊥CD,∠DAC=60°,AB=BC=AC,E是PD的中点,F为ED的中点.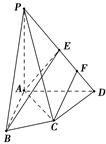
(1)求证:平面PAC⊥平面PCD;
(2)求证:CF∥平面BAE.
已知向量m=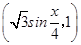 ,n=
,n=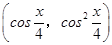 .
.
(1)若m·n=1,求cos 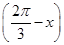 的值;
的值;
(2)记f(x)=m·n,在△ABC中,角A,B,C的对边分别是a,b,c,且满足(2a-c)cos B=bcos C,求函数f(A)的取值范围.
已知数列{an}的前三项分别为a1=5,a2=6,a3=8,且数列{an}的前n项和Sn满足Sn+m= (S2n+S2m)-(n-m)2,其中m,n为任意正整数.
(S2n+S2m)-(n-m)2,其中m,n为任意正整数.
(1)求数列{an}的通项公式及前n项和Sn;
(2)求满足 -
- an+33=k2的所有正整数k,n.
an+33=k2的所有正整数k,n.