(本小题满分13分)如图,在梯形 中,
中,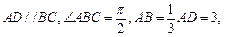


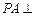 平面
平面 ,且
,且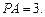
(1)求异面直线 与
与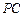 间的距离;
间的距离;
(2)求直线 与平面
与平面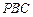 所成的角;
所成的角;
(3)已知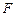 是线段
是线段 上的动点,若二面角
上的动点,若二面角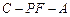 的
的
大小为 ,求AF.
,求AF.
袋中有12个小球,其中有外形,重量一样的红球、黑球、黄球、绿球.从中任取一球得到红球的概率是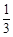 ,得到黑球或黄球的概率是
,得到黑球或黄球的概率是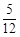 ,得到黄球或绿球的概率也是
,得到黄球或绿球的概率也是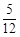 ,分别试求得到黑球、黄球、绿球的概率各是多少?
,分别试求得到黑球、黄球、绿球的概率各是多少?
在集合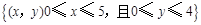 内任取一个元素,能使代数式
内任取一个元素,能使代数式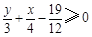 的概率是多少?
的概率是多少?
连续10次抛掷一枚骰子,结果都是出现1点,你认为这枚骰子均匀吗?
从一箱产品中随机地抽取一件产品,设事件A为“抽到一等品”,事件B为“抽到二等品”,事件C为“抽到三等品”,且已知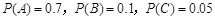 .求下列事件的概率:
.求下列事件的概率:
(1)事件D“抽到的是一等品或二等品”;
(2)事件E“抽到的是二等品或三等品”.
假设人的某一特征(如眼睛大小)是由他的一对基因所决定的,以d表示显性基因,r表示隐性基因,则具有dd基因的人为纯显性,具有rr基因的人是纯隐性,具有rd基因的人为混合性.纯显性与混合性的人都表露显性基因决定的某一特征,孩子从父母身上各得到一个基因,假定父母都是混合性.
问:(1)一个孩子有显性基因决定的特征的概率是多少?
(2)两个孩子中至少有一个有显性基因决定的特征的概率是多少?