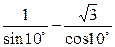（本小题满分13分）已知数列{an}，定义
（n∈N+）是数列{an}的倒均数． （1）若数列{an}的倒均数是
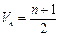，求数列{an}的通项公式；（2）若等比数列{bn}的首项为–1，公比为q =
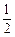，其倒均数为Vn，问是否存在正整数m，使得当n≥m(n∈N+)时，Vn<–16恒成立？若存在，求m的最小值；若不存在，请说明理由．
(本小题满分12分)
已知函数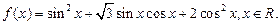
(1)求函数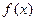
的最小正周期；
(2)当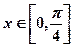
时，求函数f (x) 的最大值与最小值及相应的
值。
某营养师要求为某个儿童预订午餐和晚餐.已知一个单位的午餐含12个单位的碳水
化合物，6个单位的蛋白质和6个单位的维生素C;一个单位的晚餐含8个单位的碳
水化合物，6个单位的蛋白质和10个单位的维生素C.另外，该儿童这两餐需要的营状中
至少含64个单位的碳水化合物和42个单位的蛋白质和54个单位的维生素C.
如果一个单位的午餐、晚餐的费用分别是2.5元和4元，那么要满足上述的营养要求，
并且花费最少，应当为该儿童分别预订多少个单位的午餐和晚餐？
(本题满分14分)
某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中，随机抽取了100名电视
观众，相关的数据如下表所示：
| 文艺节目 |
新闻节目 |
总计 |
|
| 20至40岁 |
40 |
18 |
58 |
| 大于40岁 |
15 |
27 |
42 |
| 总计 |
55 |
45 |
100 |
（1）由表中数据直观分析，收看新闻节目的观众是否与年龄有关？
（2）用分层抽样方法在收看新闻节目的观众中随机抽出5名，大于40岁的观众应该
抽取几名？
（3）在上述抽取的5名观众中任取出2名，求恰有1名观众年龄20岁至40岁的概率。
在△ABC中，已知B=45°,D是BC边上的一点，
AD=10,AC=14,DC=6，求AB的长.
（本题共12分，每小题6分）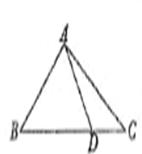
（1）证明 
（2）化简 