某篮球队与其他6支篮球队依次进行6场比赛,每场均决出胜负,设这支篮球队与其他篮球队比赛胜场的事件是独立的,并且胜场的概率是 .
.
(1)求这支篮球队首次胜场前已经负了两场的概率;
(2)求这支篮球队在6场比赛中恰好胜了3场的概率;
(3)求这支篮球队在6场比赛中胜场数的期望和方差.
已知函数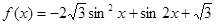 .
.
(1)求函数f(x)的最小正周期和单调增区间;
(2)在给出的直角坐标系中,画出函数y=f(x)在区间[0,π]上的图象.
如图△ABC中,已知点D在BC边上,且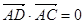 ,
,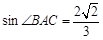 ,
,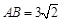 ,
,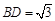 .
.
(1)求AD的长;
(2)求cosC.
在△ABC中,中线长AM=2.
(1)若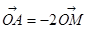 ,求证:
,求证: ;
;
(2)若P为中线AM上的一个动点,求 的最小值.
的最小值.
下表数据是水温度x(℃)对黄酮延长性y(%)效应的试验结果,y是以延长度计算的,且对于给定的x,y为变量.
| x(℃) |
300 |
400 |
500 |
600 |
700 |
800 |
| y(%) |
40 |
50 |
55 |
60 |
67 |
70 |
(1)求y关于x的回归方程;
(2)估计水温度是1 000 ℃时,黄酮延长性的情况.
(可能用到的公式: ,
, ,其中
,其中 、
、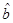 是对回归直线方程
是对回归直线方程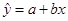 中系数
中系数 、
、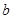 按最小二乘法求得的估计值)
按最小二乘法求得的估计值)
为了解学生身高情况,某校以10%的比例对全校700名学生按性别进行分层抽样调查,测得身高情况的统计图如下:
(1)估计该校学生身高在170~185 cm之间的概率;
(2)从样本中身高在180~190 cm之间的男生中任选2人,求至少有1人身高在185~190 cm之间的概率.