

(本小题满分14分)
已知函数 ,数列
,数列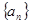 满足
满足 .
.
(Ⅰ)求数列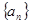 的通项公式
的通项公式 ;
;
(Ⅱ)求 ;
;
(Ⅲ)求证: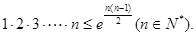
(本小题满分14分)已知椭圆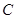 以
以 为焦点,且离心率
为焦点,且离心率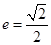 .
.
(Ⅰ)求椭圆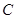 的方程;
的方程;
(Ⅱ)过 点斜率为
点斜率为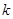 的直线
的直线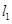 与椭圆
与椭圆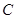 有两个不同交点
有两个不同交点 ,求
,求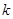 的范围。
的范围。
(Ⅲ)设椭圆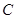 与
与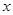 轴正半轴、
轴正半轴、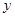 轴正半轴的交点分别为
轴正半轴的交点分别为 ,是否存在直线
,是否存在直线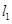 ,满足(Ⅱ)中的条件且使得向量
,满足(Ⅱ)中的条件且使得向量 与
与 垂直?如果存在,写出
垂直?如果存在,写出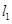 的方程;如果不存在,请说明理由。
的方程;如果不存在,请说明理由。
(本小题满分14分)如图,四棱锥P-ABCD是底面边长为1的正方形,PD⊥BC,PD=1,PC= .
.
PD=1,PC= ,PD⊥BC。
,PD⊥BC。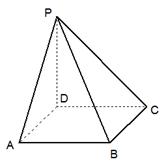
(Ⅰ)求证:PD⊥面ABCD;
(Ⅱ)求二面角A-PB-D的大小.
(本小题满分12分)现要围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需要维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:米),修建此矩形场地围墙的总费用为y(单位:元)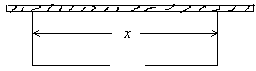
(1)将y表示为x的函数;
(2)试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用。
(本小题满分12分)已知函数 .
.
(1)求函数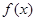 的最小正周期和最大值;(2)求
的最小正周期和最大值;(2)求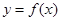 在R上的单调区间.
在R上的单调区间.