(本小题满分12分)
在一个盒子中,放有标号分别为1,2,3的三张卡片,现从这个盒子中,有放回地先后抽得两张卡片的标号分别为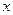 、
、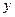 ,设
,设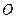 为坐标原点,点
为坐标原点,点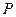 的坐标为
的坐标为 ,记
,记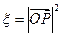 .
.
(I)求随机变量 的最大值,并求事件“
的最大值,并求事件“ 取得最大值”的概率;
取得最大值”的概率;
(II)求随机变量 的分布列和数学期望.
的分布列和数学期望.
已知数列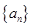 是各项均为正数的等差数列,其中
是各项均为正数的等差数列,其中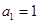 ,且
,且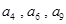 成等比数列;数列
成等比数列;数列 的前
的前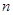 项和为
项和为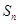 ,满足
,满足 .
.
(Ⅰ)求数列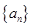 ,
, 的通项公式;
的通项公式;
(Ⅱ)如果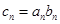 ,设数列
,设数列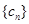 的前
的前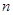 项和为
项和为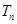 ,是否存在正整数
,是否存在正整数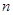 ,使得
,使得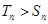 成立,若存在,
成立,若存在,
求出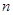 的最小值,若不存在,说明理由.
的最小值,若不存在,说明理由.
已知椭圆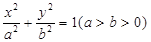 上的点
上的点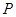 到左右两焦点
到左右两焦点 的距离之和为
的距离之和为 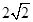 ,离心率为
,离心率为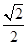 .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)过右焦点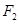 的直线
的直线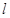 交椭圆于
交椭圆于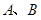 两点.
两点.
(ⅰ)若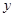 轴上一点
轴上一点 满足
满足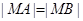 ,求直线
,求直线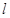 斜率
斜率 的值;
的值;
(ⅱ)是否存在这样的直线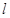 ,使
,使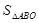 的最大值为
的最大值为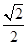 (其中
(其中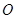 为坐标原点)?若存在,求直线
为坐标原点)?若存在,求直线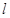 方
方
程;若不存在,说明理由.
设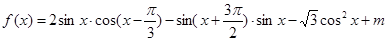 在
在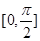 上的最大值为3
上的最大值为3
(Ⅰ)求 的单调递增区间;
的单调递增区间;
(Ⅱ)在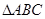 中,内角
中,内角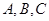 的对边分别为
的对边分别为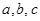 ,且
,且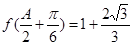 ,
, ,求
,求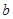 及
及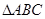 的面积.
的面积.
(本小题满分14分)已知函数 (
( ).
).
(1)讨论 的单调性;
的单调性;
(2)若 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围(
的取值范围( 为自然常数);
为自然常数);
(3)求证


 (
( ,
, ).
).
(本小题满分13分)已知椭圆
 (
(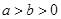 )的离心率为
)的离心率为 ,
, 是椭圆的焦点,点
是椭圆的焦点,点 ,直线
,直线 的斜率为
的斜率为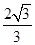 ,
, 为坐标原点.
为坐标原点.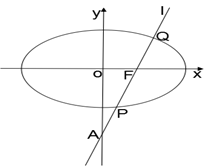
(1)求椭圆 的方程;
的方程;
(2)设过点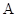 的直线与
的直线与 相交于
相交于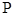 、
、 两点,当
两点,当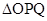 的面积最大时,求
的面积最大时,求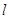 的方程.
的方程.