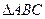 的三内角
的三内角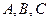 所对边的长分别为
所对边的长分别为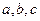 ,已知
,已知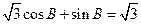 ,
,
(1)已知函数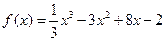 ,
,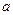 、
、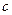 是方程
是方程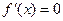 的两根,求
的两根,求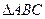 的外接圆的半径.
的外接圆的半径.
(2)若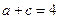 ,求
,求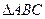 的最大值;
的最大值;
(3)若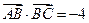 ,求
,求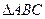 的周长的最小值.
的周长的最小值.
(满分12分)已知 为偶函数,曲线
为偶函数,曲线 过点
过点 ,且
,且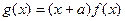 .
.
(Ⅰ)若曲线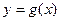 有斜率为0的切线,求实数
有斜率为0的切线,求实数 的取值范围
的取值范围
(Ⅱ)若当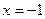 时函数
时函数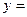
 取得极大值,且方程
取得极大值,且方程 有三个不同的实数解,求实数
有三个不同的实数解,求实数 的取值范围.
的取值范围.
(满分12分)函数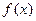 的定义域为
的定义域为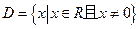 ,且满足对于任意的实数
,且满足对于任意的实数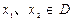 ,有
,有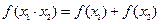 .
.
(Ⅰ)求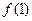 的值; (Ⅱ)判断
的值; (Ⅱ)判断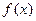 的奇偶性并证明;
的奇偶性并证明;
(I II)若
II)若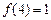 ,且
,且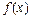 在
在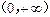 上是增函数,解关于
上是增函数,解关于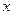 的不等式
的不等式 .
.
(满分12分) 已知函数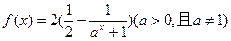 .
.
(Ⅰ)求函数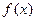 的反函数解析式;
的反函数解析式;
(Ⅱ)判断函数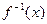 的奇偶性;
的奇偶性;
(III)当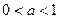 时,
时, 解不定式
解不定式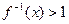 .
.
(满分12分)设函数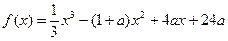 ,其中常数a>1.
,其中常数a>1.
(Ⅰ)讨论f(x)的单调性;
(Ⅱ)若当x≥0时, f(x)>0恒成立,求a的取值范围.
f(x)>0恒成立,求a的取值范围.
某高级中学共有学生2000名,各年级男、女生人数如下表:
| 高一年级 |
高二年级 |
高三年级 |
|
| 女生 |
373 |
x |
y |
| 男生 |
377 |
370 |
z |
已知在全校学生中随机抽取1名,抽到高二年级女生的概率是0.19.
(Ⅰ)求x的值;
(Ⅱ)现 用分层抽样的方法在全校抽取48名学生,问应在高三年级抽取多少名?
用分层抽样的方法在全校抽取48名学生,问应在高三年级抽取多少名?