点 与点
与点 的距离比它到直线
的距离比它到直线 的距离小1,求点
的距离小1,求点 的轨迹。
的轨迹。
(本题满分14分,第1小题6分,第2小题8分)
已知函数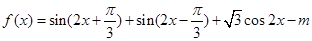 ,x∈R,且f(x)的最大值为1.
,x∈R,且f(x)的最大值为1.
(1) 求m的值,并求f(x)的单调递增区间;
(2) 在△ABC中,角A、B、C的对边a、b、c,若 ,且
,且 ,试判断△ABC的形状.
,试判断△ABC的形状.
(本题满分12分,第1小题6分,第2小题6分)
已知集合A={x| | x–a | < 2,xÎR },B={x|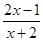 <1,xÎR }.
<1,xÎR }.
(1) 求A、B;
(2) 若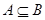 ,求实数a的取值范围.
,求实数a的取值范围.
(本题满分18分,第1小题4分,第2小题6分,第3小题8分)
已知数列{an}满足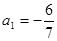 ,
,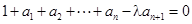 (其中λ≠0且λ≠–1,n∈N*),
(其中λ≠0且λ≠–1,n∈N*), 为数列{an}的前
为数列{an}的前 项和.
项和.
(1) 若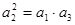 ,求
,求 的值;
的值;
(2) 求数列{an}的通项公式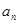 ;
;
(3) 当 时,数列{an}中是否存在三项构成等差数列,若存在,请求出此三项;若不存在,请说明理由.
时,数列{an}中是否存在三项构成等差数列,若存在,请求出此三项;若不存在,请说明理由.
(本题满分16分,第1小题4分,第2小题6分,第3小题6分)
设椭圆的中心为原点O,长轴在x轴上,上顶点为A,左、右焦点分别为F1、F2,线段OF1、OF2的中点分别为B1、B2,且△AB1B2是面积为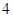 的直角三角形.过B1作直线l交椭圆于P、Q两点.
的直角三角形.过B1作直线l交椭圆于P、Q两点.
(1) 求该椭圆的标准方程;
(2) 若 ,求直线l的方程;
,求直线l的方程;
(3) 设直线l与圆O:x2+y2=8相交于M、N两点,令|MN|的长度为t,若t∈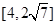 ,求△B2PQ的面积
,求△B2PQ的面积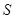 的取值范围.
的取值范围.
(本题满分14分,第1小题6分,第2小题8分)
已知函数 ,其中常数a > 0.
,其中常数a > 0.
(1) 当a = 4时,证明函数f(x)在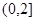 上是减函数;
上是减函数;
(2) 求函数f(x)的最小值.