已知双曲线的两条渐近线都过坐标原点,且都与以点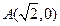 为圆心,
为圆心, 为半径的圆相切,又该双曲线的一个顶点是点
为半径的圆相切,又该双曲线的一个顶点是点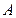 关于直线
关于直线 的对称点。(1)求此双曲线的方程;(2)若直线
的对称点。(1)求此双曲线的方程;(2)若直线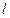 过
过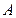 点,且与直线
点,且与直线 垂直,在双曲线上求一点
垂直,在双曲线上求一点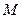 ,使
,使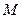 到此直线的距离为
到此直线的距离为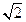 。
。
已知过点A(1,1)且斜率为-m(m>0)的直线l与x、y轴分别交于P、Q两点,过P、Q两点作直线2x+y=0的垂线,垂足为R、S,求四边形PRSQ的面积的最小值.
某运输公司接受了向抗洪抢险地区每天至少送180 t支援物资的任务,该公司有8辆载重为6 t的A型卡车与4辆载重为10 t的B型卡车,有10名驾驶员,每辆卡车每天往返次数为A型卡车4次,B型卡车3次,每辆卡车每天成本费为A型卡车320元,B型卡车504元.请你给出该公司调配车辆的方案,使公司所花的成本费最低.
如左下图,在一段直的河岸同侧有A、B两个村庄,相距5 km,它们距河岸的距离分别为3 km、6 km.现在要在河边修一抽水站并铺设输水管道,同时向两个村庄供水.如果预计修建抽水站需8.25万元(含设备购置费和人工费),铺设输水管每米需用24.5元(含人工费和材料费).现由镇政府拨款30万元,问A、B两村还需共同自筹资金多少,才能完成此项工程?(准确到100元)(参考数据: =8.06,
=8.06, =9.85,
=9.85, =3.28,
=3.28, =6.57)
=6.57)

已知直线l:x+y-2=0,一束光线过点P(0, +1),以120°的倾斜角投射到l上,经过l反射,求反射光线所在直线的方程.
+1),以120°的倾斜角投射到l上,经过l反射,求反射光线所在直线的方程.
由方程|x|+|y-1|=2确定的曲线所围成的图形的面积是多少?