已知函数 的图象与
的图象与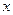 轴切于
轴切于 点,求
点,求 的极值。
的极值。
已知首项为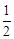 的等比数列{an}是递减数列,其前n项和为Sn,且S1+a1,S2+a2,S3+a3成等差数列.
的等比数列{an}是递减数列,其前n项和为Sn,且S1+a1,S2+a2,S3+a3成等差数列.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若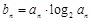 ,数列{bn}的前n项和Tn,求满足不等式
,数列{bn}的前n项和Tn,求满足不等式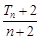 ≥
≥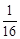 的最大n值.
的最大n值.
已知向量a=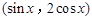 ,b=
,b=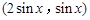 ,设函数
,设函数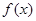 =a
=a b.
b.
(Ⅰ)求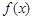 的单调递增区间;
的单调递增区间;
(Ⅱ)若将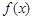 的图象向左平移
的图象向左平移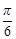 个单位,得到函数
个单位,得到函数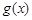 的图象,求函数
的图象,求函数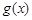 在区间
在区间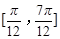 上的最大值和最小值.
上的最大值和最小值.
已知圆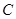 的圆心在直线
的圆心在直线 上,且与直线
上,且与直线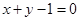 相切于点
相切于点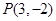 .
.
(Ⅰ)求圆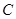 方程;
方程;
(Ⅱ)点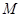
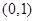 与点
与点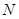 关于直线
关于直线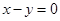 对称.是否存在过点
对称.是否存在过点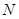 的直线
的直线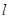 ,
,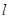 与圆
与圆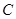 相交于
相交于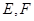 两点,且使三角形
两点,且使三角形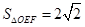 (
(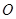 为坐标原点),若存在求出直线
为坐标原点),若存在求出直线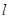 的方程,若不存在用计算过程说明理由.
的方程,若不存在用计算过程说明理由.
如图,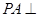 平面
平面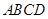 ,
, 是矩形,
是矩形,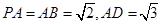 ,点
,点 是
是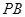 的中点,点
的中点,点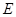 是边
是边 上的动点.
上的动点.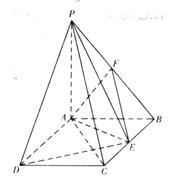
(Ⅰ)求三棱锥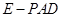 的体积;
的体积;
(Ⅱ)当点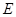 为
为 的中点时,试判断
的中点时,试判断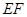 与平面
与平面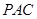 的位置关系,并说明理由;
的位置关系,并说明理由;
(Ⅲ)证明:无论点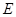 在边
在边 的何处,都有
的何处,都有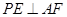 .
.
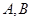 两城相距
两城相距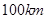 ,在两地之间距
,在两地之间距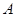 城
城 处
处 地建一核电站给
地建一核电站给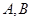 两城供电.为保证城市安全,核电站距城市距离不得少于
两城供电.为保证城市安全,核电站距城市距离不得少于 .已知供电费用(元)与供电距离(
.已知供电费用(元)与供电距离(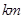 )的平方和供电量(亿度)之积成正比,比例系数
)的平方和供电量(亿度)之积成正比,比例系数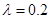 ,若
,若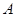 城供电量为
城供电量为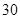 亿度/月,
亿度/月,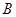 城为
城为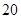 亿度/月.
亿度/月.
(Ⅰ)把月供电总费用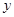 表示成
表示成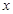 的函数,并求定义域;
的函数,并求定义域;
(Ⅱ)核电站建在距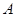 城多远,才能使供电费用最小,最小费用是多少?
城多远,才能使供电费用最小,最小费用是多少?