在一次购物抽奖活动中,假设某10张券中有一等奖券1张,可获价值50元的奖品;有二等奖券3张,每张可获价值10元的奖品;其余6张没有奖。某顾客从此10张券中任抽2张,求:
(1)该顾客中奖的概率
(2)该顾客获得的奖品总价值 (元)的概率分布列和数学期望。
(元)的概率分布列和数学期望。
(本小题满分为12分)
某中学研究性学习小组,为了考察高中学生的作文水平与爱看课外书的关系,在本校高三年级随机调查了 名学生。调査结果表明:在爱看课外书的
名学生。调査结果表明:在爱看课外书的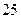 人中有
人中有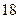 人作文水平好,另
人作文水平好,另 人作文水平一般;在不爱看课外书的
人作文水平一般;在不爱看课外书的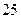 人中有
人中有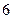 人作文水平好,另
人作文水平好,另 人作文水平一般.
人作文水平一般.
(Ⅰ)试根据以上数据建立一个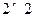 列联表,并运用独立性检验思想,指出有多大把握认为中学生的作文
列联表,并运用独立性检验思想,指出有多大把握认为中学生的作文 水平与爱看课外书有关系?
水平与爱看课外书有关系?
(Ⅱ)将其中某5名爱看课外书且作文水平好的学生分别编号为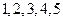 ,某
,某 名爱看
名爱看 课外书且作文水平一般的学生也分别编号为
课外书且作文水平一般的学生也分别编号为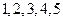 ,从这两组学生中各任选
,从这两组学生中各任选 人进行学习交流,求被选取的两名学生的编号之和为
人进行学习交流,求被选取的两名学生的编号之和为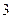 的倍数或
的倍数或 的倍数的概率.
的倍数的概率.
附: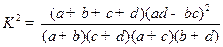
临界值表:
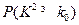 |
0. 10 |
0. 05 |
0. 025 |
0.010 |
0. 005 |
0. 001 |
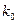 |
2. 706 |
3. 841 |
5. 024 |
6. 635 |
7. 879 |
10. 828 |
解答题(本大题共6小题,共75分,解答应写出文字说明,证明过程或演算步骤。)
16.(本小题满分为12分)
已知函数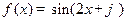 和
和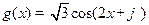 .
.
(Ⅰ)设 是
是 的极大值点,
的极大值点, 是
是 的极小值点,求
的极小值点,求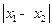 的最小值;
的最小值;
(Ⅱ)若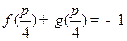 ,且
,且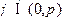 ,求
,求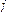 的值.
的值.
(本小题满分14分)
已知函数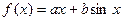 ,当
,当 时,
时, 取得极
取得极 小值
小值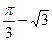 .
.
(1)求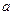 ,
,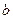 的值;
的值;
(2)设直线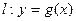 ,曲线
,曲线 .若直线
.若直线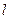
 与曲线
与曲线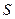 同时满足下列两个条件:
同时满足下列两个条件:
①直线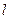 与曲线
与曲线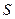 相切且至少有两个
相切且至少有两个 切点;
切点;
②对任意 都有
都有 .则称直线
.则称直线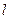 为曲线
为曲线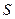 的“上夹线”.
的“上夹线”.
试证明:直线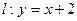 是曲线
是曲线 的“上夹线”.
的“上夹线”.
(3)记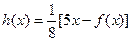 ,设
,设 是方程
是方程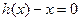 的实数
的实数 根,若对于
根,若对于 定义域中任意的
定义域中任意的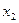 、
、 ,当
,当 ,且
,且 时,问是否存在一个最小的正整数
时,问是否存在一个最小的正整数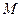 ,使得
,使得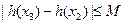 恒成立,若存在请求出
恒成立,若存在请求出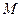 的值;若不存在请说明理由.
的值;若不存在请说明理由.
(本小题满分13分)
已知抛物线 :
: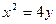 的焦点为
的焦点为 ,过点
,过点 作直线
作直线 交抛物线
交抛物线 于
于 、
、 两点;椭圆
两点;椭圆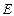 的中心在原点,焦点在
的中心在原点,焦点在 轴上,点
轴上,点 是它的一个顶点,且其离心率
是它的一个顶点,且其离心率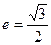 .
.
(1)求椭圆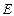 的方程;
的方程;
(2)经过 、
、 两点分别作抛物线
两点分别作抛物线 的切线
的切线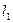 、
、 ,切线
,切线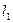 与
与 相交于点
相交于点 .证明:
.证明: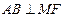 ;
;
(3) 椭圆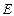 上是否存在一点
上是否存在一点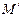 ,经过点
,经过点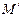 作抛物线
作抛物线 的两条切线
的两条切线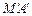 、
、 (
(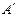 、
、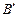 为切点),使得直线
为切点),使得直线 过点
过点 ?若存在,求出抛物线
?若存在,求出抛物线 与切线
与切线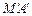 、
、 所围成图形的面积;若不存在,试说明理由
所围成图形的面积;若不存在,试说明理由 .
.
执行下面框图所描述的算法程序,记输出的一列数依次为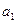 ,
,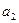 ,…,
,…,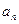 ,
,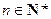 ,
,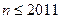 .
.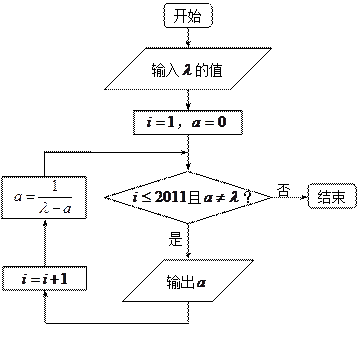
(1)若输 入
入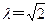 ,写出输出结果;
,写出输出结果;
(2)若输入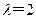 ,求数列
,求数列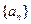 的通项公式;
的通项公式;
(3)若输入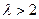 ,令
,令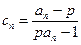 ,求常数
,求常数 (
(
 ),使得
),使得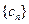 是等比数列.
是等比数列.