型企业人力资源部为了研究企业员工工作积极性和对待企业改革的关系,随机抽取了189名员工进行调查,其中支持企业改革的调查者中,工作积极的54人,工作一般的32人,而不太赞成企业改革的调查者中,工作积极的40人,工作一般的63人.
(1) 根据以上数据建立一个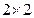 的列联表;
的列联表;
(2) 对于人力资源部的研究项目,根据以上数据可以认为企业的全体员工对待企业改革的态度与其工作积极性是否有关系?
附表:
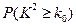 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(本小题满分14分)
已知函数 ,
, 为实数)有极值,且在
为实数)有极值,且在 处的切线与直线
处的切线与直线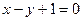 平行.
平行.
(1)求实数a的取值范围;
(2)是否存在实数a,使得函数 的极小值为1,若存在,求出实数a的值;若不存在,请说明理由;
的极小值为1,若存在,求出实数a的值;若不存在,请说明理由;
(本小题满分14分)
为积极响应国家“家电下乡”政策的号召,某厂家把总价值为10万元的A、B两种型号的电视机投放市场,并且全部被农民购买。若投放的A、B两种型号的电视机价值都不低于1万元,农民购买A、B两种型号的电视机将按电视机价值的一定比例给予补贴,补贴方案如下表所示,设投放市场的A、B型号电视机的价值分别为 万元,
万元, 万元,农民得到的补贴为
万元,农民得到的补贴为 万元,解答以下问题.
万元,解答以下问题.
| A型号 |
B型号 |
|
| 电视机价值(万元) |
 |
 |
| 农民获得补贴(万元) |
 |
 |
(1) 用 的代数式表示
的代数式表示
(2) 当 取何值时,
取何值时,  取最大值并求出其最大值(精确到0.1,参考数据:
取最大值并求出其最大值(精确到0.1,参考数据: )
)
(本小题满分14分)
如图,四边形 为矩形,
为矩形,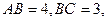 且
且 平面
平面 ,
, 为
为 上的点,且
上的点,且 平面
平面
(1)设点 为线段
为线段 的中点,点
的中点,点 为线段
为线段 的中点,求证:
的中点,求证: ∥平面
∥平面

(2)求证 

(3)当 时,求三棱锥
时,求三棱锥 的体积。
的体积。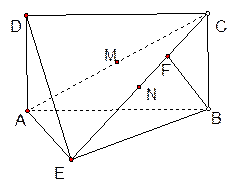
(本小题满分12分)
先阅读以下不等式的证明,再类比解决后面的问题
若 ,则
,则 .
.
证明:构造二次函数
将 展开得:
展开得:

 对一切实数
对一切实数 恒有
恒有 ,且抛物线的开口向上
,且抛物线的开口向上 ,
, .
.
(Ⅰ)类比猜想:
若 ,则 .
,则 .
(在横线上填写你的猜想结论)
(Ⅱ)证明你的猜想结论.
(本小题满分12分)
在 中,已知
中,已知 ,且
,且 .
.
(Ⅰ)求 的大小。
的大小。
(Ⅱ)证明 是等边三角形
是等边三角形
k