求经过点 的直线,且使
的直线,且使 ,
, 到它的距离相等的直线方程。
到它的距离相等的直线方程。
已知点A、B的坐标分别是A(0,-1),B(0,1),直线AM、BM相交于点M,且它们的斜率之积是-t,t∈(0,1].求M的轨迹方程,并说明曲线的类型.
已知函数f(x)= (m,n∈R)在x=1处取得极大值2.
(m,n∈R)在x=1处取得极大值2.
(1)求函数f(x)的解析式;
(2)求函数f(x)的极值;
(3)设函数g(x)=x2-2ax+a,若对于任意x2∈[-1,1],总存在x1∈R,使得g(x2)≤f(x1),求实数a的取值范围.
已知双曲线C: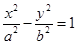 (a>b>0)的一个焦点为
(a>b>0)的一个焦点为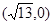 ,离心率为
,离心率为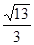 .
.
(1)求双曲线C的标准方程;
(2)若动点P(x0,y0)为双曲线外一点,且点P到双曲线C的两条切线相互垂直,求点P的轨迹方程。
数列{an}满足a1+2a2+22a3+…+2n-1an=4n.
⑴求通项an;
⑵求数列{an}的前n项和 Sn.
已知向量 =(sin(
=(sin(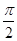 +x),
+x),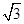 cosx),
cosx), =(sinx,cosx), f(x)=
=(sinx,cosx), f(x)=  ·
· .
.
⑴求f(x)的最小正周期和单调增区间;
⑵如果三角形ABC中,满足f(A)=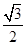 ,求角A的值.
,求角A的值.