7人按要求排成一纵队,其中A、B、C三人的前后顺序一定,那么有多少种不同的排法?
（本小题满分12分）已知椭圆C：
（a>b>0）的焦距为4，其短轴的两个端点与长轴的一个端点构成正三角形．
（1）求椭圆C的标准方程．
（2）设F为椭圆C的左焦点，T为直线x＝－3上任意一点，过F作TF的垂线交椭圆C于点P，Q．
①证明：OT平分线段PQ（其中O为坐标原点）；
②当
最小时，求点T的坐标．
（本小题满分12分）已知椭圆C：
的左、右焦点分别是F1、F2，离心率为e．直线l：y=ex+a与x轴、y轴分别交于A、B两点，M是直线l与椭圆C的一个公共点，P是点F1关于直线l的对称点，设
。
（1）证明：
；
（2）确定
的值，使得
是等腰三角形。
（本小题12分）如图所示，已知四棱锥P-ABCD的底面为直角梯形，AB//DC，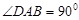
，PA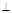
底面ABCD，且PA=AD=DC=
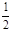AB=1，M是PB的中点。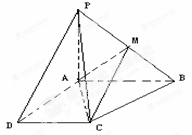
（1）证明：面PAD面PCD；
（2）求AC与PB所成角的余弦值。
（本小题13分）已知A为椭圆
上的点，过A作AB
x轴，垂足为B，延长BA到C使得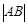
=
。
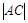（1） 求点C的轨迹方程；
（2）直线l过点D （2，3）且与点C的轨迹只有一个交点，求l 的方程。
（本小题13分）已知：一个圆锥的底面半径为R，高为H，在其中有一个高为x的内接圆柱．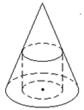
（1）求圆柱的侧面积；
（2）x为何值时，圆柱的侧面积最大。