某项选拔共有三轮考核,每轮设有一个问题,能正确回答问题者进入下一轮考试,否则即被淘汰,已知某选手能正确回答第一、二、三轮的问题的概率分别为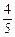 、
、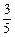 、
、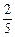 ,且各轮问题能否正确回答互不影响.
,且各轮问题能否正确回答互不影响.
(Ⅰ)求该选手被淘汰的概率;
(Ⅱ)该选手在选拔中回答问题的个数记为ξ,求随机变量ξ的分布列与数数期望.(注:本小题结果可用分数表示)
(本小题满分12分)在 中,内角
中,内角 ,
, ,
, 的对边分别为
的对边分别为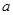 ,
,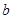 ,
, ,且
,且 .
.
(1)求角 的值;
的值;
(2)若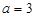 ,
, ,求
,求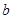 ,
, 的值.
的值.
(本小题满分12分)已知函数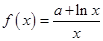 在
在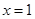 处取得极值.
处取得极值.
(1)求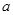 的值,并讨论函数
的值,并讨论函数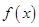 的单调性;
的单调性;
(2)当 时,
时,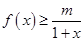 恒成立,求实数
恒成立,求实数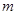 的取值范围.
的取值范围.
(本小题满分12分)在某次质量抽测后一数学老师随机抽取了30位(其中男、女各15名)同学的成绩,得出如下表,假设80分为“优秀”,否则为“不优秀”.
| 性别 |
成绩 |
| 男 |
83 81 96 68 83 77 86 97 78 64 85 91 90 99 82 |
| 女 |
74 70 68 86 92 72 76 78 78 64 86 66 79 68 70 |
(1)根据以上数据,试估计本次质量抽测数学科的优秀率(保留小数后三位);
(2)完成下列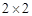 列联表:
列联表:
| 优秀 |
不优秀 |
合计 |
|
| 男 |
 |
||
| 女 |
 |
||
| 合计 |
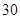 |
(3)根据(2)中表格数据,利用独立性检验的方法判断,能否在犯错误的概率不超过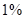 的前提下,认为“数学成绩”与“性别”有关?(其中
的前提下,认为“数学成绩”与“性别”有关?(其中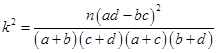 )
)
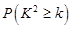 |
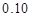 |
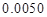 |
 |
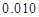 |
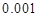 |
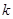 |
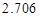 |
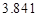 |
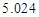 |
 |
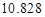 |
(本小题满分12分)已知数列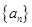 首项为1,
首项为1,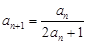 .
.
(1)证明:数列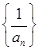 是等差数列,并求
是等差数列,并求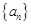 的通项公式;
的通项公式;
(2)记数列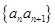 的前
的前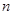 项和为
项和为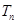 ,证明:
,证明: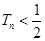 .
.
(本小题满分10分)选修4-5:不等式选讲.
设函数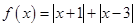 .
.
(1)求不等式 的解集;
的解集;
(2)若存在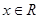 使得
使得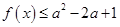 成立,求实数
成立,求实数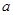 的取值范围.
的取值范围.