某条公共汽车线路沿线共有11个车站(包括起点站和终点站),在起点站开出的一辆公共汽车上有6位乘客,假设每位乘客在起点站之外的各个车站下车是等可能的.求:
(I)这6位乘客在其不相同的车站下车的概率;
(II)这6位乘客中恰有3人在终点站下车的概率;
(本小题满分14分)
已知二次函数 满足以下两个条件:
满足以下两个条件:
①不等式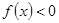 的解集是(-2,0)②函数
的解集是(-2,0)②函数 在
在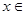
 上的最小值是3
上的最小值是3
(Ⅰ)求 的解析式;
的解析式;
(Ⅱ)若点
 在函数
在函数 的图象上,且
的图象上,且
(ⅰ)求证:数列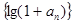 为等比数列
为等比数列
(ⅱ)令 ,是否存在正实数
,是否存在正实数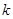 ,使不等式
,使不等式 对于一切的
对于一切的 恒成立?若存在,指出
恒成立?若存在,指出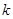 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
(本小题满分12分)
某港口O要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时,轮船位于港口的O北偏西30°且与该港口相距20海里的A处,并正以30海里/小时的航行速度沿正东方向匀速行驶. 假设该小艇沿直线方向以v海里/小时的航行速度匀速行驶,经过t小时与轮船相遇.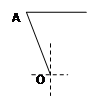
(Ⅰ)若希望相遇时小艇的航行距离最小,则小艇航行时间应为多少小时?
(Ⅱ)为保证小艇在30分钟内(含30分钟)能与轮船相遇,试确定小艇航行速度的最小值;
(本小题满分12分)如图所示,某房地产开发公司计划在一楼区内建造一个长方形公园ABCD,公园由长方形的休闲区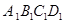 (阴影部分)和环公园人行道组成.已知休闲区
(阴影部分)和环公园人行道组成.已知休闲区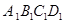 的面积为4000 m 2,人行道的宽分别为4 m和10 m.
的面积为4000 m 2,人行道的宽分别为4 m和10 m.
( I )设休闲区的长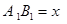 m ,求公园ABCD所占面积
m ,求公园ABCD所占面积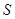 关于 x 的函数
关于 x 的函数 的解析式;
的解析式;
(Ⅱ)要使公园ABCD所占总面积最小,休闲区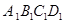 的长和宽该如何设计?
的长和宽该如何设计?
(本小题满分12分)
福州市某大型家电商场为了使每月销售空调和冰箱获得的总利润达到最大,对某月即将出售的空调和冰箱进行了相关调查,得出下表:
| 资金 |
每台空调或冰箱所需资金 (百元) |
月资金最多供应量 (百元) |
|
| 空调 |
冰箱 |
||
| 进货成本 |
30 |
20 |
300 |
| 工人工资 |
5 |
10 |
110 |
| 每台利润 |
6 |
8 |
问:该商场如果根据调查得来的数据,应该怎样确定空调和冰箱的月供应量,才能使商场获得的总利润最大?总利润的最大值为多少元?
(本小题满分12分)
已知△ABC的内角A、B、C所对的边分别为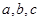 且
且 .
.
( I ) 若 ,求周长的最小值; (Ⅱ) 若
,求周长的最小值; (Ⅱ) 若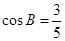 ,求边
,求边 的值.
的值.