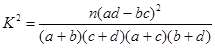(本小题满分12分)(原创题)
在平面直角坐标系中,已知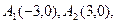
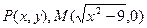 ,若实数
,若实数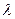 使向量
使向量
 。
。
(1)求点 的轨迹方程,并判断
的轨迹方程,并判断 点的轨迹是怎样的曲线;
点的轨迹是怎样的曲线;
(2)当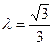 时,过点
时,过点 且斜率为
且斜率为 的直线与此时(1)中的曲线相交的另一点为
的直线与此时(1)中的曲线相交的另一点为 ,能否在直线
,能否在直线 上找一点
上找一点 ,使
,使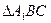 为正三角形(请说明理由)。
为正三角形(请说明理由)。
一台机器使用的时间较长,但还可以使用,它按不同的转速生产出来的某机械零件有一些会有缺点, 每小时生产有缺点零件的多少,随机器的运转的速度而变化,下表为抽样试验的结果:
| 转速x(转/秒) |
16 |
14 |
12 |
8 |
| 每小时生产有缺点的零件数y(件) |
11 |
9 |
8 |
5 |
(Ⅰ)画出散点图;
(Ⅱ)如果y对x有线性相关关系,求回归直线方程;
(Ⅲ)若实际生产中,允许每小时的产品中有缺点的零件最多为10个,那么机器的运转速度应控制在什么范围内?
参考公式: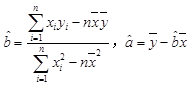
实数x分别取什么值时,复数z=x2+x-6+(x2-2x-15)i对应的点Z在:
(1)第三象限;
(2)第四象限;
(3)直线x-y-3=0上?
用分析法证明: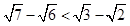
(本小题满分13分)万州区2007年至2013年农村居民家庭纯收入y(单位:千元)的数据如下表:
(Ⅰ)求y关于t的线性回归方程;
(Ⅱ)利用(Ⅰ)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘法估计公式分别为: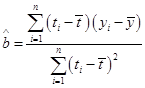 ,
,
(本小题满分13分)某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体1000名学生中随机抽取了若干名学生的体检表,并得到如下直方图: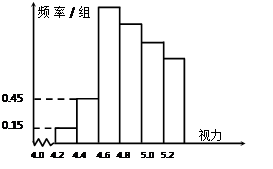
(Ⅰ)若直方图中前三组的频率成等比数列,后四组的频率成等差数列,试估计全年级视力在5.0以下的人数;
(Ⅱ)学习小组成员发现,学习成绩突出的学生,近视的比较多,为了研究学生的视力与学习成绩是否有关系,对年级名次在1~50名和951~1000名的学生进行了调查,得到如下数据:
| 年级名次 是否近视 |
1~50 |
951~1000 |
| 近视 |
41 |
32 |
| 不近视 |
9 |
18 |
根据表中的数据,能否在犯错的概率不超过0.05的前提下认为视力与学习成绩有关系?
(Ⅲ)在(Ⅱ)中调查的100名学生中,按照分层抽样在不近视的学生中抽取了9人,进一步调查他们良好的护眼习惯,并且在这9人中任取3人,记名次在1~50名的学生人数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
附:
| P(K2≥k) |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
| k |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |